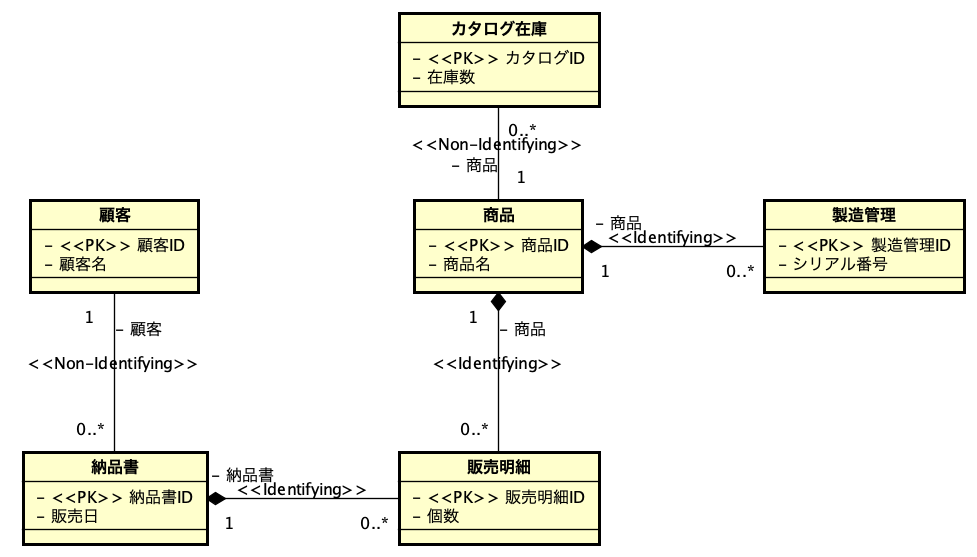
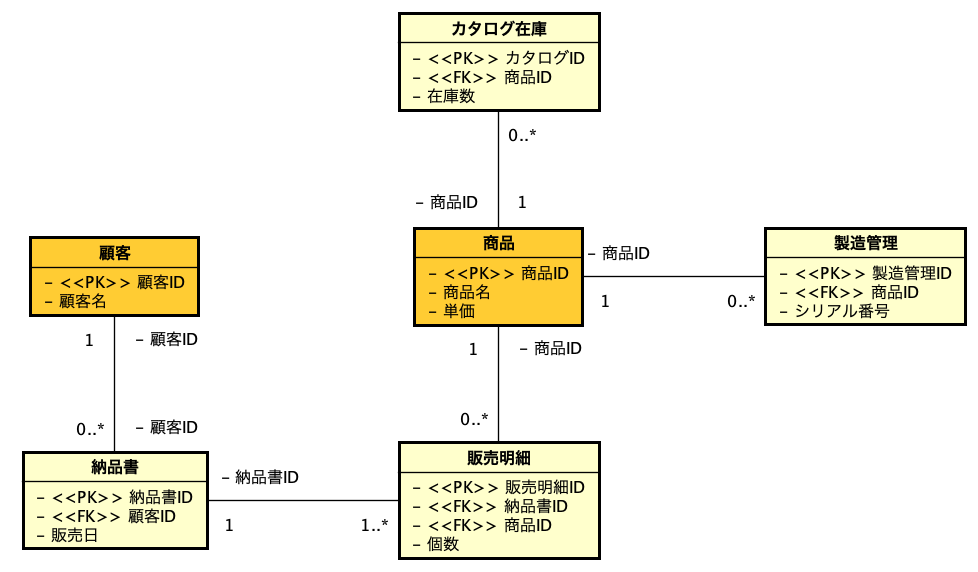
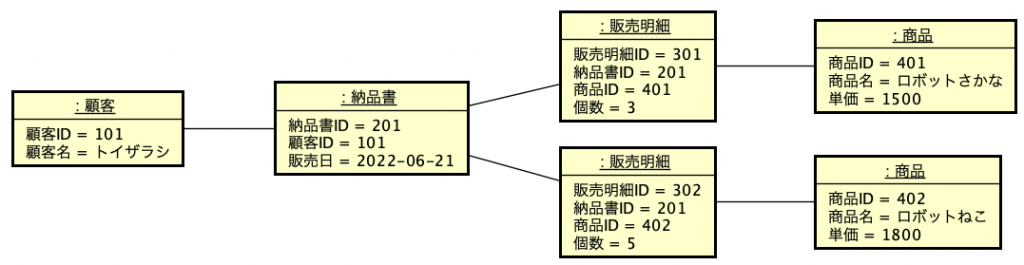
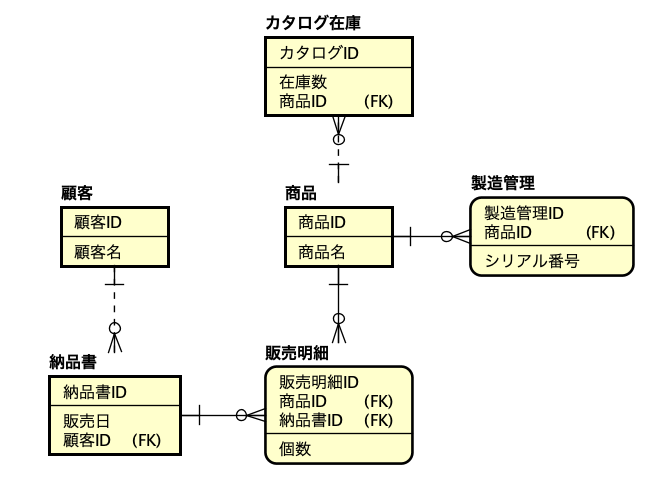
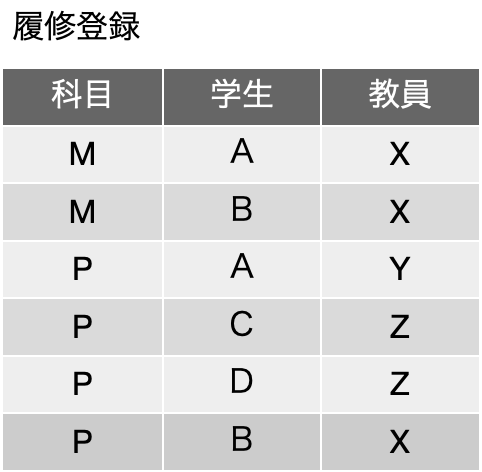
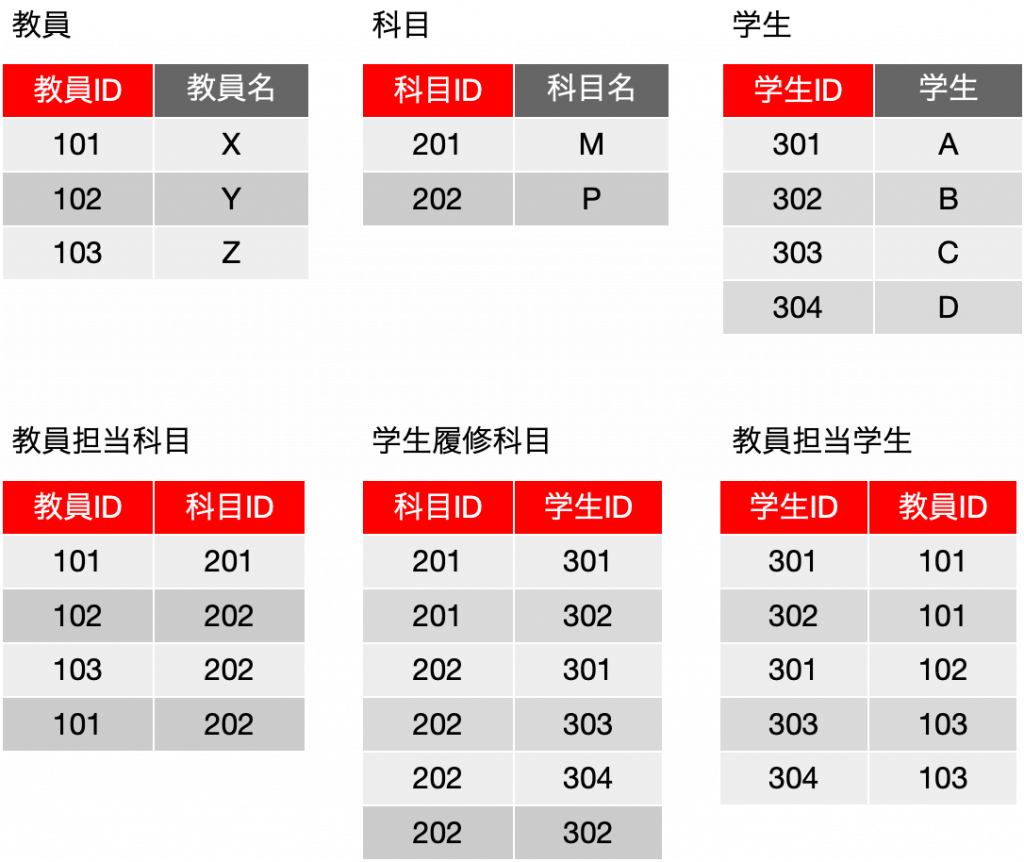
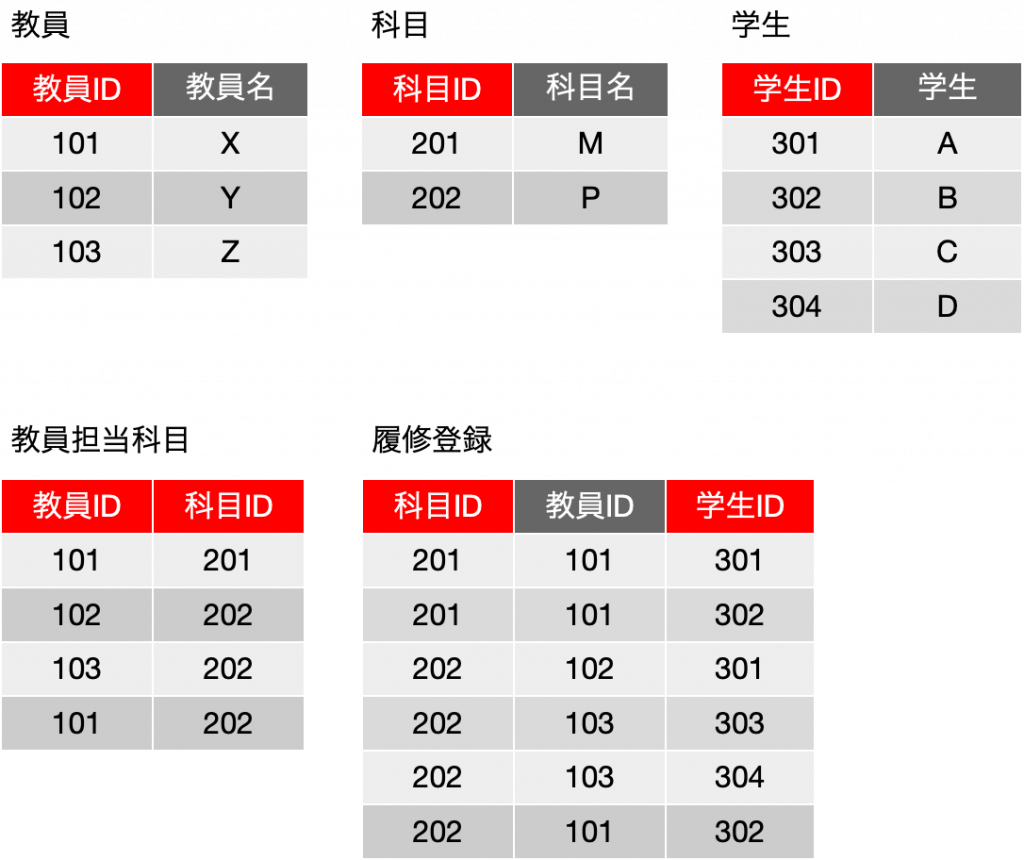
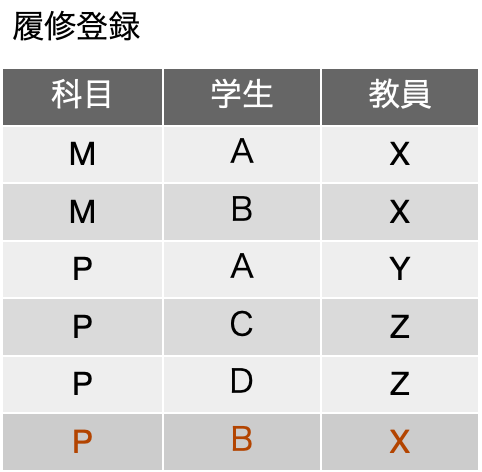
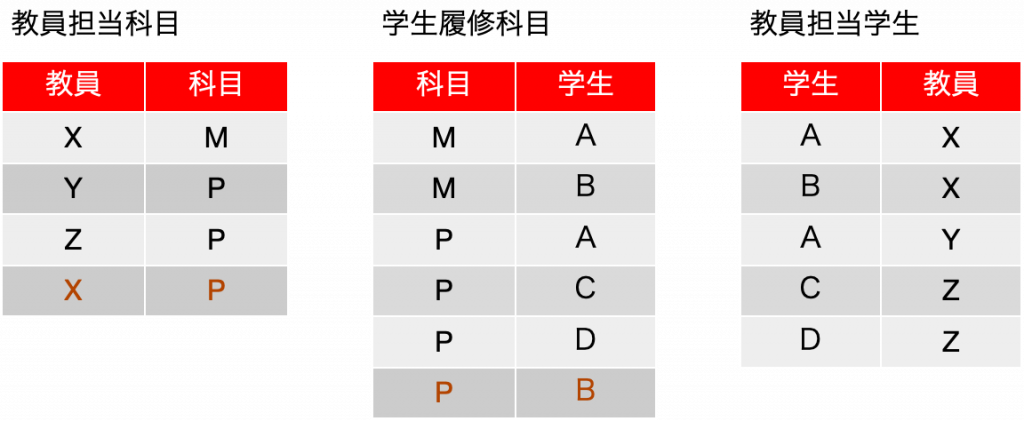
一時期、サロゲートキーについての議論が盛り上がったこともありますが、古い本を紐解くと、2006年に初版が出ている「Refactoring Databases: Evolutionary Database Design (Scott W. Ambler and Pramod J. Sadalage)」あたりにそこそこ詳しく書いてあったりもしました。サロゲートキー(surrogate key)とは、人工的に作り出したキーフィールドで、例えば連番の機能を使ってあるフィールドに自動入力するなどして、確実に主キーとなる単独のフィールドをテーブルに用意しておく手法です。最近は、UUIDを文字列型のフィールドに入れるような場合も見られます。連番の場合はバグがや運用ミスがなければ確実にレコードごとに異なる値が振られます。UUIDだと、異なるシステムで生成されたレコードを統合しても、やはり一意な値になっていることが十分に期待できるので、少々のパフォーマンス低下はあるとしても、データベースを分散して運用する場合や、後から統合が必要な複数のデータベースの運用では便利に利用できるでしょう。
しかしながら、サロゲートキーは元々データに存在しない、まさに人工的なキーであって、モデルそのものに存在するのが間違いであるという考え方もできます。人工的に値を追加していいのであれば、なんでもありになってしまい統制が取れません。本来、業務上保存が必要なデータがどんな振る舞いをするのかということを示すのが主キーであり候補キーであるという考え方であり、その主キーの存在を手がかりにしているのが正規化の理論だったりするので、無駄なものを許容しないという見方は分かります。かくして、サロゲートキーは使わないことを「複合キー(Compsite Keys)で運用する」ような呼び方になっているのですが、この場合は複数のキーフィールドであるということではなく、複数のキーフィールドであっても本来のデータにある情報からキーフィールドを選択するべきであるということを言いたい用語です。つまり、英語のCompositeを単に複合と訳すと、複数っぽいニュアンスが垣間見えてしまうというところです。なお、「人工キー(Artificial Keys)」の対比で、「自然キー(Natural Keys)」と呼ぶ場合もあります。
それぞれのメリット、デメリットは順次紹介しますが、概して、複合キーであるべき論は、データモデリングの立場から出ている意見です。これに対して、実装側の意見としては、サロゲートキーあるいは「単独のキーフィールド」というべきかもしれませんが、そういう状態が望ましい場合が多々あるというところでしょうか。どこかで激論があるとしたら、単に立場の違いということだけですが、IT業界の不思議な分業体制がいまだに根付いている感もあるので、やはり「職種による対立」に発展しかねないテーマでもあります。ですが、時代は協調を求めています。相手の立場に立って考えることがなんと言っても必要です。
まず、データモデリングの立場から、サロゲートキーがなくても主キーを決定できる場合は、不要なものがない方がモデルを示す情報としてはより良いという単純な考え方ができます。不要なものは不要だということですね。一方、データモデリングの立場であってもある状況であればサロゲートキーを許すというか、それをモデルとして認識せざるを得ないような場合です。それは、本当にデータに主キーが存在しないような場合です。極端な例では、センサーからの送達データなのか、どこかでエクスポートしたデータなのか、フィールドが {時刻, 場所, 温度} のような場合はどうでしょうか? 普通、時刻あるいは時刻と場所でキーになりそうな感じではありますが、強引ですが、同一時刻、同一場所で測定されていることもあるような場合はもうお手上げです。その場合は、サロゲートキーを付与するしかありません。インポート時に付与するなどの方法があり、キーとしてはサロゲートキーを使うということをモデルに記述する必要が出てきます。このような事例として、データウェアハウスでのデータ管理でサロゲートキーを使うというのは基本的なテクニックとして古いから認識されています。いずれにしても、こういう「どうしようもない場合」以外はサロゲートキーを使う必要はないという立場です。
一方、サロゲートキーは容認、あるいは必要という立場は、まず、実装上の立場から言えます。システムの内部では、「レコードを特定する」という場面がよく発生します。わかりやすいのは、一覧を表示し、「編集」ボタンをクリックすると、そのレコードの編集画面が出るような場合です。ここで、画面には見えていないかもしれませんが、一覧の各行のに対して「どのレコードか」を特定するデータがどこかに隠されています。そして、ボタンをクリックした時、その特定のためのデータをシステムは次のページに引き渡して、そのページでは、示されたデータを表示します。そして、そのページが編集可能なページであるとしたら、あるフィールドを変更した結果をデータベースに伝えるために、どのレコードなのかを覚えておいてそれを利用します。もちろん、そのどのレコードなのかに使えるデータは主キーです。これが {時刻, 場所} のようなキーを使うとの{計測結果ID}のような単一のサロゲートキーを使っている場合とを比較すると、当然ながら、システム開発は後者の方が容易で確実、つまりソフトウエアの品質保証を確保しやすいと言えるのです。もちろん、「プロの開発者ならそれくらい対処しろや」と言いたいかもしれませんが、テーブルごとにキーが違っていると、その都度微妙に違うプログラムを作ることになりますが、全てのテーブルがサロゲートキーを主キーにしているというルールでデータベースが構築されていれば、どのレコードもプログラム上の扱いは均一化されるので、やはりミスや出戻りが少なくなることが期待できます。さらには、現在はフレームワークを使った開発が一般的になり、フレームワークでは様々な処理が自動化されているのですが、そのような場面ではサロゲートキーの利用が必須だったり、あるいはフレームワークが勝手に作ってしまうような場合もあるかもしれません。仮に複合キーもOKとしても、フレームワークの内側で、文字列データの比較などを適切に行っているのかということも気になる部分であhあって、それなりにデバッグはされているとは思いますが、謎の関連付けが発生しかねないという懸念も持ってしまいます。
すごく荒っぽい言い方をすれば、開発する側はサロゲートキーの方が都合がいいのです。単一のレコードの特定に使う場合もありますが、ロジックを組むような場合で、いくつかのレコードの集合を記録しておいて、ある値を求めて、後からそれらのレコードを全部更新するような場合、つまりは主キーを配列に残して処理を進めます。そのような場合でも、複合キーの場合とサロゲートキーの場合では、当たり前ですが、後者の方が容易であることは言うまでもありません。また、連番で整数になっているフィールドの値だと、気軽に検証ができます。UUIDも文字列ではありますが、長さや正規表現のマッチングで検証は可能です。そういうちょっとした安心を増やすことも、サロゲートキーではやりやすいと言えます。
Refactoring Databasesでは、以上のようなことを「複雑さの回避が可能」と表現しています。そして、この書籍でもう1つ重要なことが書いてあって、「ビジネスドメインの変更を受けにくい」と述べています。要するに、仕様が変わって主キーだったと思っていたものが違いました、あるいはもっとフィールドを増やさないと主キーになりませんと言うことがあったとして、サロゲートキーで運用してれば、「主キーの変更」と言う大ごとは起こらないと言うことです。複合キーによる主キーを変更するとなると、おそらくプログラム側の変更は結構大変ですし、変更しきれずバグがダラダラと残りそうな雰囲気がぷんぷんしてきます。
ところで、このような仕様変更の話が出てくると、必ず言われるのが、「それは最初に仕様をまとめたやつが認識できなかったのが悪い」などといった意見です。後でも議論しますが、確かにデータベース設計は初期段階に決めて変更しないようにするという鉄則のようなものはあるのですが、なぜ仕様変更となるのかということを改めて考えてみる必要があります。もちろん、設計者がボーッとしていて気づいていないことで、後から変更が必要になるというのは困ったものですが、それを避ける方法としてはレビューをきちんと行うということに尽きるかと思います。開発者全員が釈然と対処したとしても、システム発注側が認識していないことについては、どうしても、開発途中にその要求が具体化されるということがあり、それによってデータベース設計の変更が伴うことはよくあります。仕様書に従って作っているだけだと開き直るのは、IT業界内での理想論であって顧客ビジネスをしている限りは完全に開き直るのは悪とされます。ともかく、発注側が全てを把握しているとは限らないのです。この前提は忘れてはいけません。発注側が、業務を全て理解して分析可能な知識があるとは誰も保証していません。なので、ある程度動くシステムができたところで、「あっ!」ってなることは十分あり得る話です。一方で、ビジネス環境の変化も早くなりつつあり、開発している間にビジネス環境の変化はあり得ます。それに追随することを顧客は望んでいます。要するに、設計変更を受け入れる余地がないような開発の段取りでは、現在では受け入れてもらえないのではないでしょうか。もちろん、そのために別の機能の実装は諦めるとか、費用な納期を見直すという交渉を行うなどの、技術的なことを超える対処は必要になりますが、現在ではそういう時にどういう問題があってどうすべきかは知識として蓄積されていると言えるかと思います。仕様変更の必要が生じたとき、前向きに取り組むかどうかの問題です。そのような中、設計変更が生じたとしても、仕様作成の担当者がミスったという見方は自分の責任じゃないのだと言いたいのだと思いますが、なんだかブラックな空気を感じます。
実際、筆者でも、「データ内のフィールドを主キーフィールドにしてやばいことになった」ということを何度も経験しています。製造番号や商品番号が重複しているのは、まだ序の口でした。ある案件で、早いうちに製造番号が、なぜか10年経過すると同じ番号がわり当たると言うルールで運用されていて、それは変えないという決定がなされたので、当然ながら、サロゲートキーを割り当てることになります。その案件では、商品番号も怪しいと思っていたら、やっぱり重複があって、というか、1レコードで管理したいものに商品番号はユニークに振られていなかったので、やはりサロゲートキーを設定しました。このような、よくある設計例であるような「◯◯番号」であっても、実データを読み込むと「あー!重複している」ということは結構ありました。ですが、一番印象に残るのは、「◯◯◯の◯◯番号」です。伏せ字ですみません。これを書くと色々不味そうなので、お許しを。この番号は常識的には重複はないと思われるものです。このシステム、ある程度開発された結果を元に作れというのが至上命令だったので、痕跡を残すためにも途中から手を入れ始めました。そして、この番号がキーになっていたんです。その時の開発スタッフ同士で、かなり悩みました。この番号がキーだけど、ほんとにキーにしていいのか? いっそのことサロゲートキーに置き換えるか、そうだとしたら、かなり変更しないといけない。などなど議論して、結局、常識的にこの番号はユニークだろうということで、そのまま使いました。この「常識」って疑うべきことの最優先だと思いながらも、トレードオフの理由として光っていたのです。そして、データを統合したら、なんと重複があったんです。しかも、重複回避のための番号の振り替え等はやらないと決まったらしく、これはきつい状況です。サロゲートキーにしていれば、そこで悩むことはなかったのかもしれません。ちなみに、筆者はそれが顕在化した段階では開発スタッフから外れていたので、その後どう対処したのかは聞いていません。ですが、当然最初の段階で、その番号には絶対に重複はないということを発注側から聞いており、常識的にそうなので信じてしまい、データの確認もせず(というか、できなかった)、ということだったので、最初からサロゲートキーにしておくべき案件だったと後から噛み締めるのでした。
一方、サロゲートキーを設定したとしても、候補キーとしてフィールドの組みがあると確実に言えるような場合は、UNIQUEをつけたインデックスを作り、それらのフィールドをキー制約に入れて、少なくとも、「同じデータの組み合わせ」が存在しないようにすることは必要になります。もちろん、必要に応じてNOT NULLによるNULL制約も設定します。サロゲートキーがあるからとそれだけPRIMARY KEY定義するだけで放置せずに、候補キーがあるとしたら、それはデータベースの設計としてケアする必要があることが一般的と考えるべきでしょう。
そのほか、パフォーマンスの議論などもあるのですが、現在のコンピュータ環境と進化したデータベースの実装では、あまり関係ないこともあるかもしれません。昔はパフォーマンス要因として大きかったものも、時代と共に変化します。もちろん、計算量を見積もって考えるということは基本ではありますので、その時代に応じたパフォーマンスの検討は必要にはなります。ちなみに、郵便事業より全国の郵便番号のデータが配布されていて、10万件を超える文字データです。筆者は大昔からこれを使っているのですが、20年前はインデックスなしではそこそこ検索に時間がかかっていましたが、10年前の段階で、インデックスの有無による検索時間の差はもうほぼないくらいになっていました。ですが、もちろん、念のためにインデックスは付けています。検索が重なる場合やパフォーマンスを落とすような検索ワード(と書きつつどんなのかわかりませんが)があったときの対処ということです。
主キーの話をFileMakerと絡めるのはかえって変な方向に行くかもしれませんが、FileMakerはある時期からテーブルのデフォルトフィールドで「主キー」という名前のフィールドを作り、当初は連番を、そして現在はUUIDを設定するようになっています。つまり、サロゲートキーそのものが既定値で作られるのです。FileMakerには、SQLにあるようなPRIMARY KEYに相当する機能はありませんし、複合フィールドのインデックスを作ることもできません。単一フィールドに対する一意性を確保することは可能です。結果的にサロゲートキーが前提としてそこで一意性を確保し、自然キーがあるとしたら、入力時の検証等をうまく働かせるなどの対処が必要になります。そのように、FileMakerでのリレーショナルデータベースの実装はある意味少し変わっているところもあります。ですが、基本、サロゲートキーを既定値にしているあたりで、サロゲートキー自体は否定されるものではないかということを示しているとも言えます。
モデリングをする側としては、「俺の素晴らしいモデルに余計なものを入れるな」と思われるかもしれませんが、実装して、完成に持ち込まないといけない立場からすると、サロゲートキーに結果的にしなければならない場面が出てくることや、複雑さを持ち込まないというあたりで、積極的に使いたいのがサロゲートキーなのです。別に実装チームはモデリングチームの成果を否定したいわけではなく、実装に都合の良いようにして欲しいだけなのです。
ちなみに、現在の複雑なシステムでは、多くは「レイヤーアーキテクチャ」というアーキテクチャパタンを踏襲した構成になっていると思います。一般にはユーザーインタフェースを最上位層、データベースを最下層として、その間を1層あるいは複数層のコントローラなどで構成し、基本的に「上から1層下への利用」にとどめるという実装を進めるのが特徴です。2層を超えることは、複雑さを回避するためやりません。下から上については、一定の制約を設けて実施できるようにしますが、よくある手法はイベント発生により、あるレイヤーのオブジェクトのメソッドがコールされるような枠組みを作っておいて、複雑な要求に応えられるようにします。このレイヤーアーキテクチャは、上から下へのコールが基本なので、高いレイヤーほど一般には変更しやすくなります。低いレイヤーを変更すると、下手をすると、上位レイヤーまで変更しなければならなくなります。そこで、よく変更が行われるユーザインタフェースやそれを受け取る上位コントローラのレイヤーを「上」に配置します。言い換えれば、データベースやそのモデルなどは「なるべく早い段階で完成させて固定化する」という方策とセットになった手法であるとも言えます。つまり、データベース設計は、後からあまり「変わらない」ことを期待しているのです。しかし、それを拡大解釈しているのかどうか、「変えない」と思っている方もいらっしゃるのかもしれません。データベース設計者を神格化しているのか、決定事項が絶対だと思っているのでしょうか? データベース設計者に特権があるわけではなく、あなたもスタッフの1人です。大体、偉い人、あるいは偉そうな人が担当していることが多いのですが、仕様変更があったらデータベース設計も含めて変更作業に着々と取り組むことが求められています。レイヤーアーキテクチャだとデータベース変更をしてはいけないわけではありません。それよりも、顧客のニーズに応えることが、より高いレベルでのゴールにあるので、変更の必要がある場合には変更すべきなのです。確かに上のレイヤーまで変更が及ぶかもしれませんが、何の整理されていないコード群に比べて。影響の範囲をグラフ(メソッド呼び出しのつながり)として把握できるので、素手で取り組むよりも遥かに効率は高いと言えます。こういったIT業界内の謎のヒエラルキーも崩れがちではありますが、そういう空気感はまだ感じるところでもあります。
正規化の理論は別の記事で詳しく述べてきていますが、意図的にサロゲートキーを使ったサンプルも載せているように、サロゲートキーを使ったからと言って、正規化の理論が崩れることはありません。ただ、主キー以外に候補キーを把握した上でないと議論はできないので、サロゲートキーだけを見ていればいいわけではありません。ですが、サロゲートキー追加しても正規化の理論が崩れないということであれば、それはそれで安心して使える材料でもあると言えるでしょう。