ボイス-コッド正規形でも十分難しいのに、さらに第四・・などとなると、もうだめだーと思われるかも知れませんが、正規形の考え方はデータベース設計の基礎でもあるので、頑張って理解しましょう。第四と第五は、大雑把な意味ではまとめて理解してもいいのですが、ここでは段階的に話を進めたいと思います。ただし、第四正規形のサンプルは、説明のためのサンプルが結構多いような気がします(その意味で言えば、全部説明っぽいとも言えるのですが)。なので、1つのサンプルを色々いじってみて、最終的に第五正規形を満たすことを考えて見たいと思います。
まず、前提として、第四、第五正規形は、3つの対象(エンティティ)が絡み合う場合が前提です。3つというのはフィールドが3つという意味ではありません。1つの表にまとまるものが3つあるという状況だと考えてください。そして、その3つの対象がそれぞれ関連性を持っているということで、少なくとも2つの関連性が存在します。あるいは3つの関連性があるかも知れません。それらを別々に表で管理しなさいというのが、実は第四、第五正規形の結論です。データが三竦み状態になるようなことはよくありませんか? もちろん、二組ずつに分解が「簡単に」できれば、多分、それは第三正規形までの議論で終わっていると思います。つまり、関数従属が2つ存在するような場合に相当するでしょう。しかし、関数従属がうまく存在してくれない場合、あるいは従属性が見つけにくいとでも言えばいいでしょうか。そういう場合が第四正規形以降で議論する対象になります。このようなケースは意外にあります。分解が難しいと思ったら、三竦みになっていないかを考えると良いでしょう。ただ、三竦みの登場人物をきちんと把握しないと間違った設計に行ってしまいます。とにかく、「事実を表にする」というのが基本です。
では、以下のような表「履修登録」を考えてみます。表の中身は、Mではなく「数学」などとそれらしく書いてもいいのですが、だんだん、こうした変数っぽく書く方がわかりやすくなってくるのは感じてもらえると思います。もちろん、ここでは、XやAは集合ではなく、何らかのデータです。基本、どれも「ラベル」ですね。入るべき文字列がどんなものか、フィールド名から明白に定義可能です。まず、学生は科目を履修するのは良いとして、その結果、{科目, 学生} について、重複するレコードは存在しないということになります。つまり、学生Aが科目Mを2つ取得するという事はなく、1つあるいは存在しないのどちらかになるので、{科目, 学生} は候補キーに含まれるべきフィールドです。教員はある科目を担当するのですが、ここではまず、単一の科目に複数の異なる教員が割り当てられているという前提で話を進めます。Mは置いておいて、科目Pは、どうやら、Y先生とZ先生の「クラス」がある模様です。大きな大学なら、必須科目なんかで同一の科目が先生ごとにいくつか開催されて、さらに所属する学科でどの先生の講義を取るかを決められているようなこともあります。そんな感じです。ともかく、そいういう場面を想定してください。科目と学生が決まれば、教員は自動的に決まるかというと、まずはそうではなく、後から教務課が適当に割り振ったという状況にしましょう。もちろん、どの先生がどの科目を担当するのかという情報がどうもこれだけだと曖昧な感じがしますが、そこは実は焦点となります。ただ、科目Pの状況を見るとYかZということになり、{科目} → {教員}という関数従属はとりあえずなさそうです。ということで、学生がどれかの科目の履修をするとしたら、教員は必ず割り当てられるということを考えれば、{科目, 学生} → {教員} という関数従属があると考えられるので、候補キー、及び主キーは{科目, 学生} となります。他に関数従属がない場合はボイス-コッド正規形を満たしているということになります。これ以上の表の分割はできないのでしょうか?
更新整合性が損なわれることはそんなに難しい話ではないと思います。今まで通りの考え方で、関数従属はとりあえず不明な感じですが、この表は、フィールドになっている3つの対象に関する関係を記述していると言えるので、例えば、3行目を削除すると、Y先生が科目Pを担当しているという情報が落ちるなど、状況は色々考えられます。
ここで、第四正規形であるかどうかを評価する指標として「多値従属性」という考え方があります。きちんと数学的に定義はされているのですが、大まかに言うと、2つの表に分解し、その分解した結果から表の結合をすることで元に戻せるという性質があれば、多値従属性があるとしています。多値従属性は、{X, Y, Z}からなる表がある場合、{X, Y} と {X, Z}の表に分解できるということでもあります。これをMD: X→→Y|Z のように書きますが、Zの存在は明確なので、「X→→Y」だけを書くことが多いようです。関数従属から矢印が1つ増えただけですね。この多値従属に関しても公理系が定義されているため、多値従属は数学的な意味で確実に証明可能な手がかりにもなりますが、ちょっと複雑なので、そういうものもあるというだけで留めます。
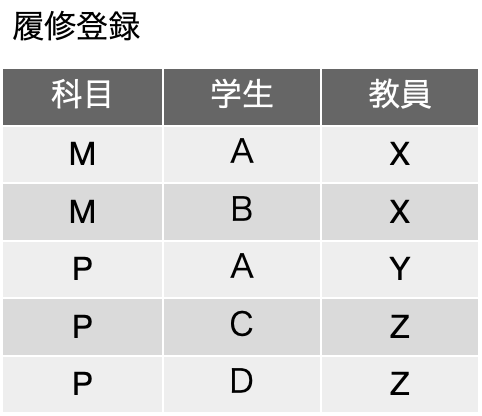
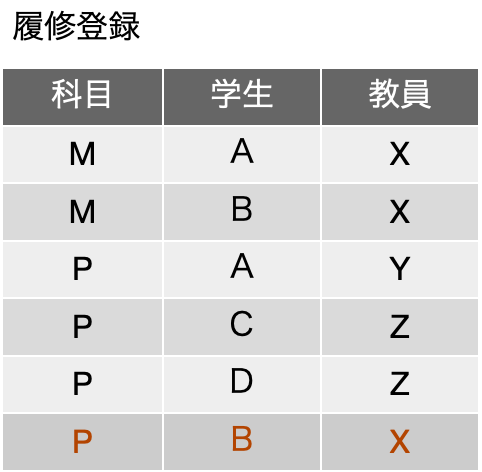
では、前の表は、分解可能でしょうか? 実はだめなんです。いや、できるかもしれません。それをこれから説明します。第四正規形に移行可能なサンプルと思ってしまった皆さん、ごめんなさい、この辺りの内容は、要するに説明が難しいのですよ。ということで、あえて、この表を3つの表にまず分解したのが以下の表です。3つのフィールドから2つのフィールドを取り出すということで、3C2 = (3 x 2) / (2 x 1) = 3つの表が出てきます。ただし、一番左の「教員担当科目」については、1行目と2行目、4行目と5行目が同一の事実を表している(前者は、教員Xが科目Mを担当するという実々)ので、レコードとして2つ存在している必要はないと考えて、同じレコードを捌きます。他はどうやらそういったレコードの重複はなさそうです。教員担当科目については、先の議論がやりやすいようにフィールドの順序が入れ替わっているので、そのつもりで見てください。
右の2つの表については、存在する2つのフィールドの組みがいずれも主キーになります。まずは、関数従属性がいずれの表にもないということを考えます。実は、学生と教員、科目と学生については、いずれも「多対多」の関係にあり、データベース設計ではそちらの考え方でテーブル設計を進める方がわかりやすいのですが、ここではともかく表を考えることにします。
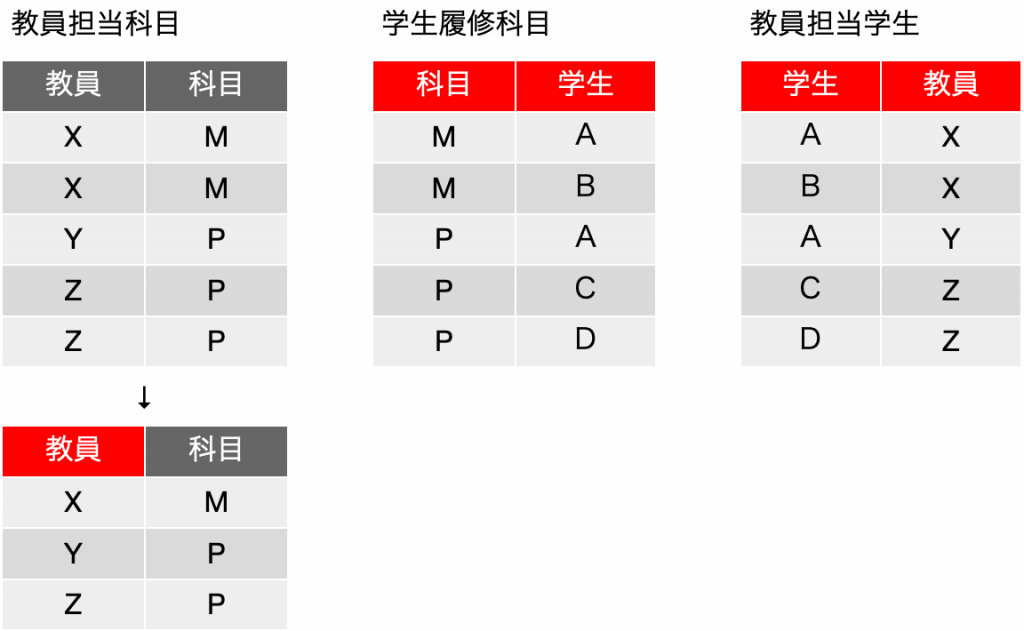
ここで、分割した表から元の表が再現できるかを、分割した表の合成をおこなってみて検討しましょう。まず、教員担当科目と学生履修科目を結合して合成してみます。手順は、左から1つレコードを取り、照合するフィールドが同じものを右側で探して、それらのフィールドをくっつけたものを結果として残す、という作業を繰り返した結果です。つまり、{X, M}に対して、右側に{M. A}があるので、{X, M, A}を結果に残します。また、右側の2行目に{M, B}があるので、{X, M, B}も残します。ここまでは元の表にあったレコードばかりです。ところが、左側の2行目{Y, P}に対して、照合をかけると科目Pのものは右側に3つあります。つまり、左側の2行目に対して、{Y, P, A} {Y, P, C} {Y, P, D}が得られます。{Y, P, A} は元の表にありましたが、{Y, P, C} {Y, P, D} は元の表にないレコードです。合成した結果を以下に示しますが、背景がピンクの行は元の表に存在しない行です。分解して戻そうとしても元には戻りませんでした。つまり、{科目} →→ {教員}|{学生} という多値従属はなかったということになります。
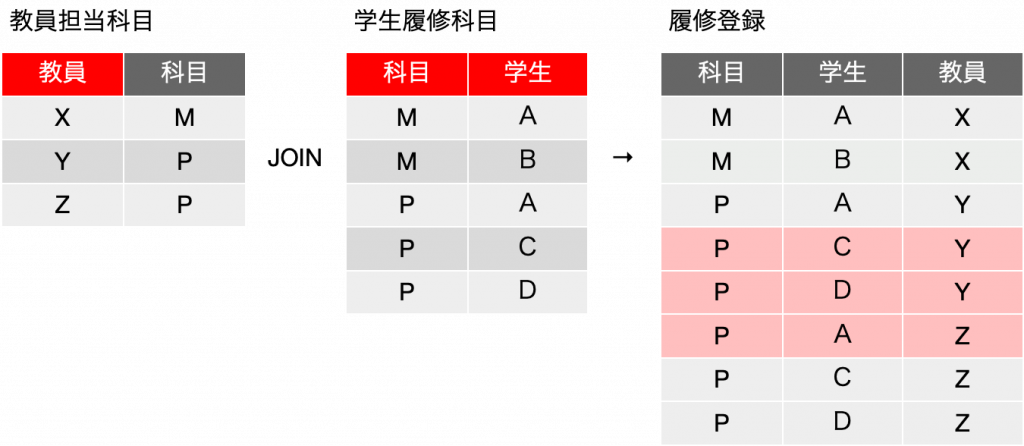
では、左端の教員担当科目と、右端の教員担当学生を、結合したらどうでしょうか。もちろん、共通の教員を元に照合をします。教員担当科目の1行目{X, M}と、教員担当学生を照合した結果、{X, M, A} {X, M, B}が得られます。2行目の{Y, P}に対しては、{Y, P, A}のひとつだけが得られます。全て行うと、確かに元の表が得られるので、現在得られているデータが全てだと仮定すると、{教員} →→ {科目}|{学生} という多値従属が存在するとも言えます。
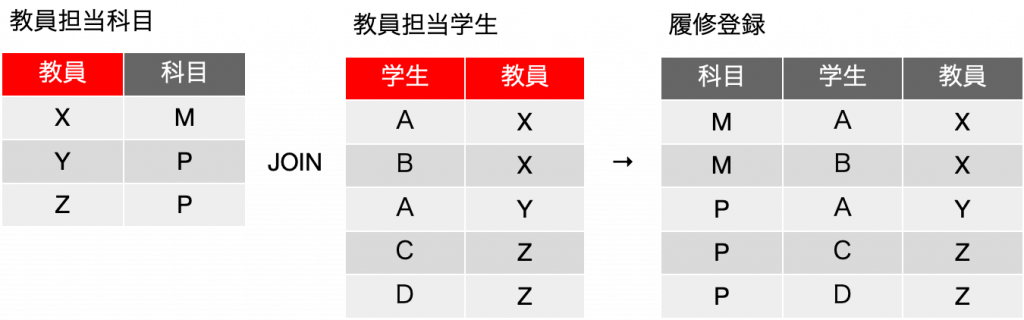
この2つの表に分解ができたとまずは結論づけます。ここで、教員担当科目はもう職員会議で決まったもので、今年は一切変更がないとします。その後、学生がどんどんと履修するのですが、例えば、E君は科目Mを取りたいとすると、事務の人が教員担当科目を見て {E, X} しか割り当てられないので、つまり、数学は1人の先生しかいないので、教員担当学生に {E, X} を追加することで、3フィールドがある履修登録表に無事1つのレコードが追加されました。F君が科目Pを取りたいとして、事務の人は、Y先生かZ先生かを決めて、例えば{F, Z}を教員担当学生の表に追加します。そして、結合した結果、履修登録では、{P, F, Z} が新たに登場します。つまり、分割した表を処理することで、元の表を処理することができるという状態になっています。
ということで、第四正規形は終わります、と言いたいところですが、そうは行きません。仮に元データが一部のデータだったらどうでしょう。ここで、反証として、元の表に、{P, B, X} が追加されたとします。物理学Pの履修者が多く、学生Bを登録したときに、既存のクラスY、Zでは賄いきれないと思って、数学のX先生にも物理学Pの担当をお願いしてクラスを増やしたような状況です。
この状況で、単純に表を3つに分割します。「教員担当科目」の表に{X, P}が増えます。学生履修科目の表にも{P, B}が増えます。教員担当学生の表には{B, X}が増えるかと思うと、元々そのレコードがあるので重複があるので追加の必要はありません。分割した表では重複するレコードは排除します。
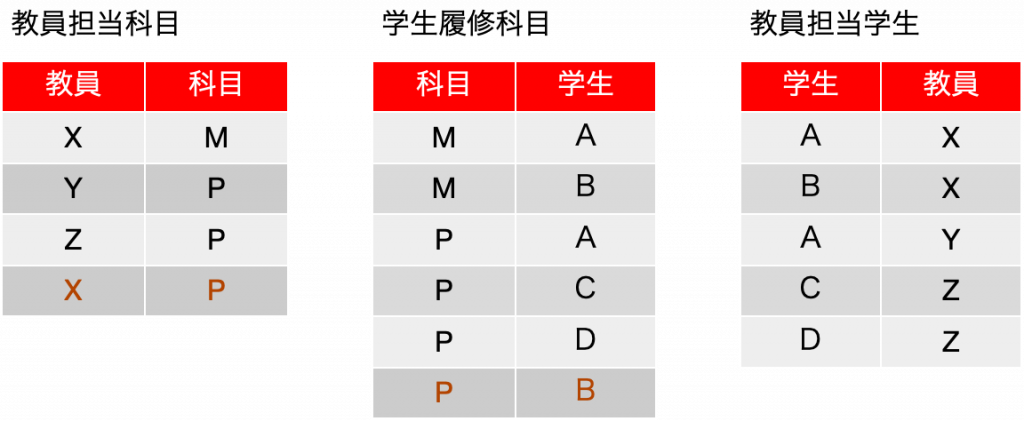
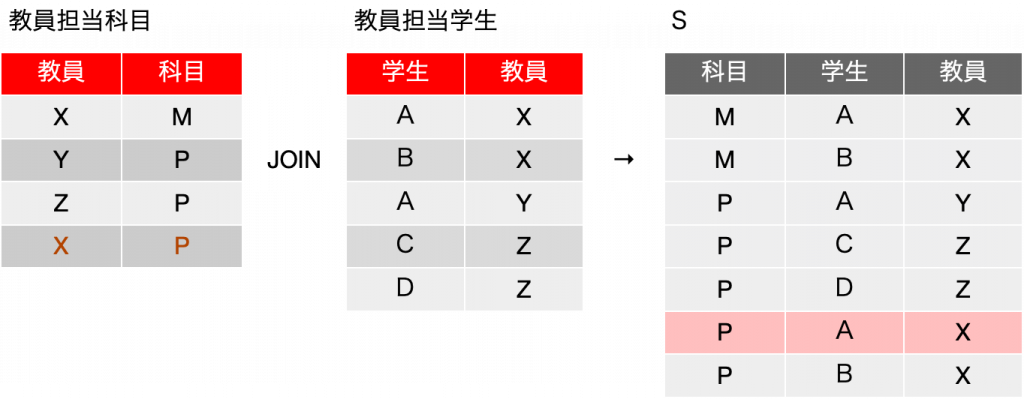
この結果、レコード追加前であれば元の表が再現できた「教員担当科目」と「教員担当学生」の結合の結果Sは、以下のようになり、余分なレコードが増えます。つまり、分解から戻しても、元の表が再現されていないので、{教員} →→ {科目}|{学生} という多値従属はやっぱりありませんでした。分解した結果を元には戻せないということからそう結論づけることができます。
ここで、すでに多値従属性はないという結論が出ている上で、第四正規化の話をしたいのですが、第四正規化の条件は、表に存在する多値従属性の左辺が全てスーパーキーであるというものです。ボイス-コッド正規形の条件に似ていますが、判定するのは関数従属性ではなく多値従属性です。
最初の表が仮に「全データ」だとしたら、{教員} →→ {科目}|{学生} という多値従属はありますが、{教員} は表に対するスーパーキーではありませんので、第四正規形ではないという結論になります。そして、多値従属があるのだからテーブルを「教員担当科目」「教員担当学生」の分離できるということになり、その結果それぞれの表は2フィールドずつになりもはや多値従属性はないので、第四正規形を満たしていると言えるということになります。第四についての厳密な議論はあえて避けます。次に説明するように、現実的な問題点は別のところにあります。
ここで、行を追加する前の履修登録について何か見落としていないかを考えます。すると、すでに答えは書いてありますが、教員担当科目の表を見ると、{教員} → {科目} という関数従属が存在していました。要求事項として出ていませんが、データを見ると明白です。つまり、ある先生は1つの科目しか担当しないという、現実にはあり得ない状況がデータにはあったのです。たまたま、そういう状況が何年か続いてシステムが動いていたとしても、突然、1人の教員が複数の科目を担当するという状況になったときその状況をデータとして表現できないことにもつながり、システムは破綻してしまいます。ですが、設計上のことを考えれば、主キーが{科目, 学生}であり、他に{教員} → {科目} という関数従属性があるとしたら、これはどこかで見たことがありますね。主キーに関係しないフィールドから、主キーの一部に関数従属があるということで、ボイス-コッド正規形を満たさないパターンです。つまり、{教員}はスーパーキーではないということで、{教員} → {科目} の関数従属に関する表を分離すれば良いということになります。ということで、正規形の世界を前進しているつもりがちょっと後退してしまいました。ここで行った「教員担当科目」と「教員担当学生」への分割は、第四正規形を満たしていないからというよりも、ボイス-コッド正規形を満たしていないからというのがより正しい言い方になります。
しかしながら、後から修正した表は、{教員} → {科目} の関数従属は存在しません。教員と科目には関係はありそうですが、どうやら多対多の関係のようです。このようなときに表に分解できないのかということになりますが、それを可能にするのが第五正規形になります。