第四正規形の説明をしたときの表を改めて示しながら、第五正規形を説明しましょう。履修科目登録は3つのフィールドがあり、それぞれ何かのルールに従って入力されているような感じでした。
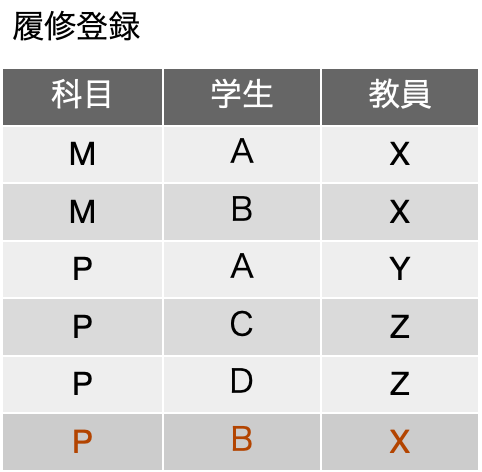
6行目を追加する前の状態で、かつ、{教員} → {科目} という関数従属性、つまりは、教員が決まれば科目は一意に決まる。つまり、ある先生は1つの科目しか持たないというルールを入れれば、「教員担当科目」が単独の表として存在でき、その表を引き算した結果は、残るフィールド「学生」と照合可能な教員フィールドを持つ「教員担当学生」の表の、これらの2つの表を結合すれば元の表が得られました。しかしながら、主キーとは関係のない関数従属性があるということで、すでにボイス-コッド正規形ではないということになりました。
ここで、この関数従属はないものとして、「教員担当科目」は、先生と科目の対応表というように仕組みを拡張したとします。その結果、前のように、X先生はMにもPにも受け持つということになります。表として分解した結果は以下の通りです。「教員担当学生」に {B, X} が追加されていないのは元々その情報が表に存在していたからです。
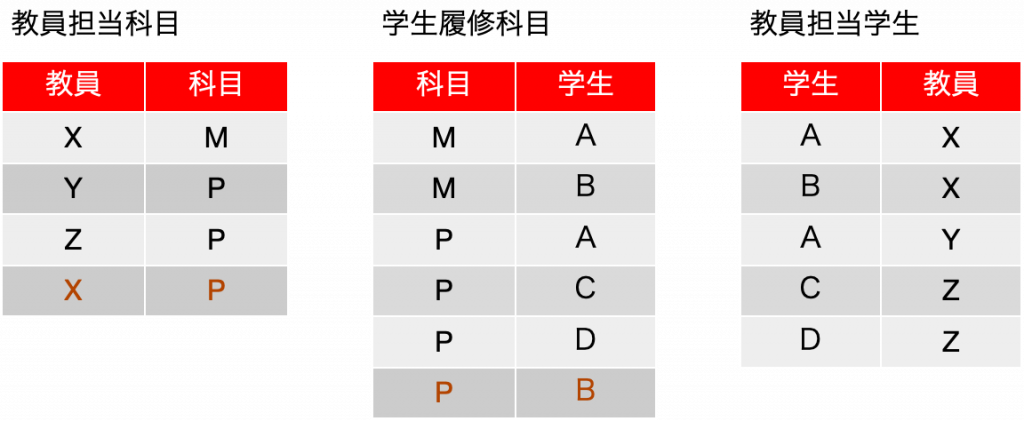
前回はこのうち、2つの表を結合していました。2つを結合すれば、少なくともフィールドは3つ揃うのでうまく元の表が合成できないかを考えたのですが、関数従属があるという前提で、その関数従属に絡んだ分割でないと元には戻りませんでした。
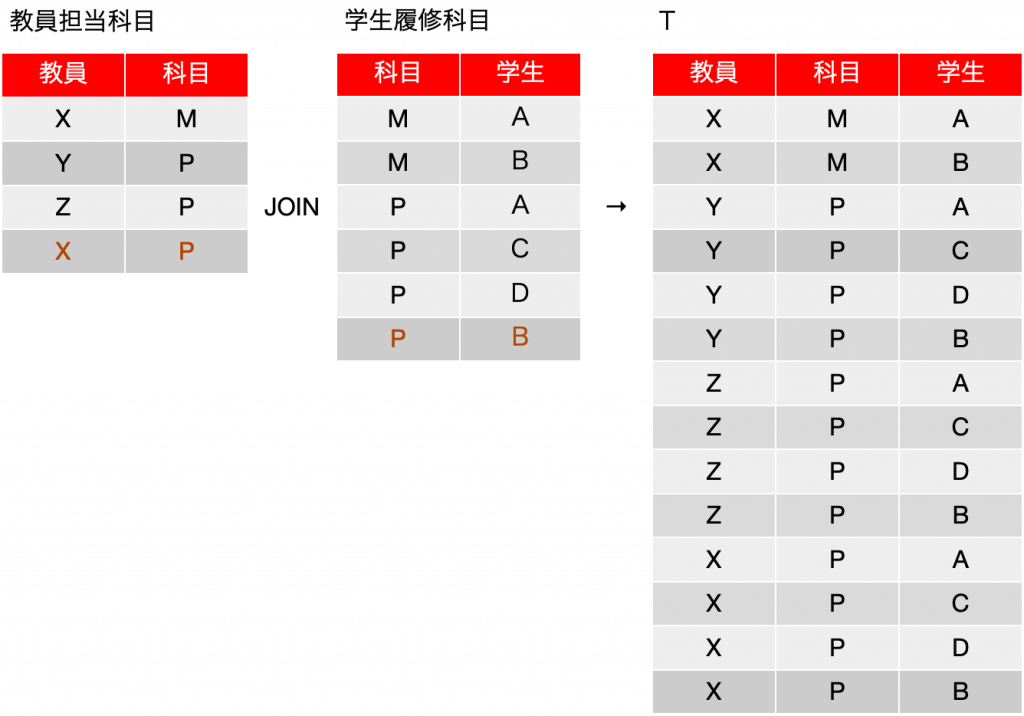
そこで、3つの表を全て結合してみます。前から順に行きましょう。まず、以下のように表Tを求めました。もちろん、元の表よりもかなり多くなっています。もちろん、科目同士を照合します。
このTに残る表を結合すると、なんと、元の表に戻ります。ここではそれぞれの表の {学生, 教員} を手がかりに照合します。Tの1行目は手がかりが {A, X} なので、教員担当学生にある {A, X} を探すとあります。もちろん、ここでフィールドを合体してもいいのですが、教員担当学生によって新たなフィールドは登場しないので、「照合可能なレコードが存在する」というのは、言い換えれば結果の表にそのまま追加されるということです。ちなみに、Tの4行目{Y, P, C}に対して、照合するフィールド{C, Y}のレコードが教員担当学生の表にあるかというとありません。ということで、照合可能なレコードがない場合は照合されるものがなかったということで消えてしまって、 Tの4行目{Y, P, C}を元にしたレコードは結果には存在しないということになります。これが結合の処理のルールです。ちょうど、「担当教員学生」の表によってあたかもフィルターのような効果が見られるということになります。
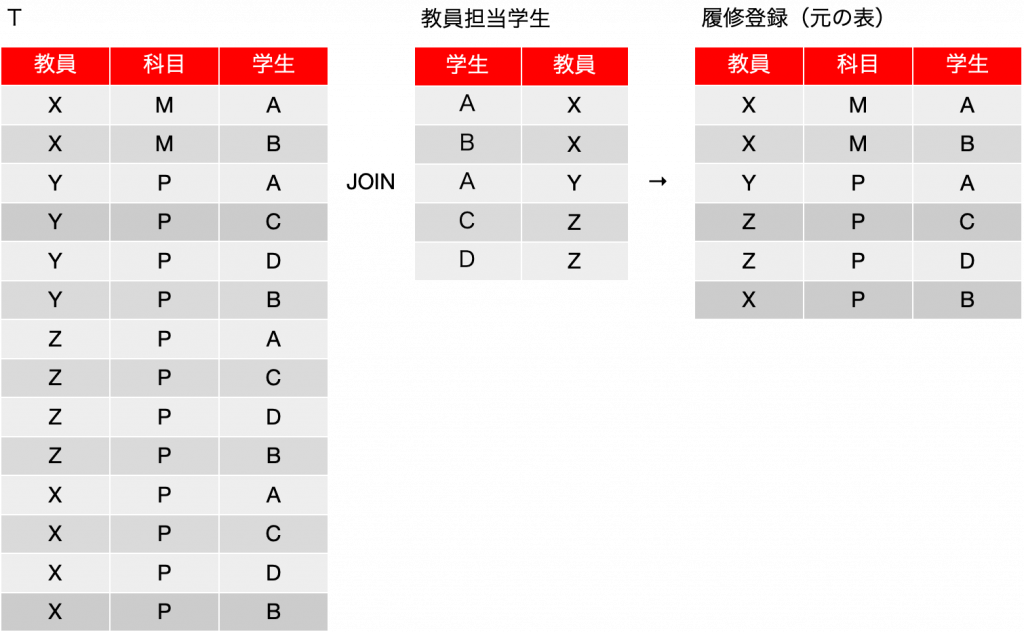
ということで、実は3つのフィールドある場合、3つのテーブルへの分割は、どうやら可能だということがわかったわけです。ざっくりと言えば、この分割をした結果が第五正規形です。もちろん、要求事項によっては前回に見たように2つで事足りかもしれません。3フィールドだから必ず3つということではありません。
第五正規形を正しく議論するとき、多値従属性をさらに拡張した結合従属性という考え方を基礎にすることになるのですが、かなり難しくなるようで、詳細が説明されていない場合が多いです。ただ、Abiteboul先生の「Foundations of Databases」での第四正規形の見出しは「無関係な情報を同一の表に入れるんじゃない」というような趣旨になっていて、言い得て妙なのではないでしょうか。第四、第五正規形のサンプルで最初に出した、3つのフィールドのある表は、ワークしそうな気はしますが、実は3つのフィールドから2つのフィールドを取り出した場合、もちろん3通りの組み合わせがあるのですが、それぞれに意味のある情報であったということになります。つまり、3つの関係性に関わる情報が、当初は1つの表に込められていたけど、それらの関係は分離できるということを第四、第五正規形は言っているのです。
3つの表に分解した結果を改めて見てみましょう。{教員, 科目}のフィールドを持つ「教員担当科目」は、教員と科目の関係なので、例えば、教員1人ずつを見ると、その先生が持つ科目の一覧になりますし、科目1つに絞り込めばその科目を担当する先生の一覧になります。つまり、教員と科目について対応関係があるかどうかということを記述している表になります。同様に「学生履修科目」は、学生がどの科目を履修しているかを表現する表です。そして、「教員担当学生」はどの先生のクラスに学生が属しているかという表になります。3つのフィールドはそれぞれ関連性がありますが、一方で、3種類の関連性があってそれらはバラバラにすることができるということになります。「教員担当学生」だけが単独で存在するのは少し違和感があるかもしれませんが、「教員担当科目」と「学生履修科目」だけでは、情報が少ないのです。つまり、この2つの対応関係だけだと、学生がどの先生のクラスなのかが確定しないということになります。
更新整合性についても検討しましょう。新たにクラスに追加するということを行うとき、「学生履修科目」と「教員担当学生」にレコードを追加することになります。これは、学生がどの科目を履修するのかという情報と、どの先生のクラスで履修するのかという2つの事実を記録するためであって、2つのレコードを記述するのは、2つの新たな関係性を記録するという意味では不整合はないと言えます。ここで、科目は自由に選べるとしても、担当する先生は「教員担当科目」によって規定された範囲でなければなりません。例えば、新たな学生が科目Mを選択するときに、その学生がZ先生であってはいけません。言い換えれば、「教員担当学生」に追加可能なレコードは、「教員担当科目」によって制限されるということになります。新たにクラスを作るとしたら、「教員担当科目」にレコードを追加しなければなりません。これは、実用上は単純なことではないでしょう。その制約をどこで解決するか、つまりUIでうまく制限するなり処理途中で確認をするなどの対処は設計上検討が必要です。
また、この表では学生Bは、2つの教科ともX先生のクラスですが、科目PはZ先生のクラスにするということになりました。では、「教員担当学生」の{B, X}を{B, Z}にするかというとそうではありません。この場合、たまたま2科目分の情報が同一だったので1レコードになったのですが、それぞれ違う先生のクラスになるということは、{B, X}はそのままにして、{B, Z}を追加する必要があります。そうすれば、表の結合で所望の表は得られるのですが、1項目の変更なのに、追加をするという必要が出てきます。つまり、クラス変更については、単に更新処理だけでは済まないということになり、ここもシステム構築の複雑さを増すことになります。つまり、データによって更新処理が異なるというのはある意味で不整合と言えるでしょう。この点は正規形によって解決できる箇所ではなく、むしろ発生した新たな問題と言えます。
このような表が欲しい場合、設計はどうすればいいでしょうか? 次回はそのことを考えてみたいのですが、少し間が開くと思います。