ボイス-コッド正規形の話はまだ続きがあるのですが、ここで少し正規形の段階を前に遡って第一正規形の話をしたいと思います。通常、関数従属性については、第二正規形以降で出てくる話なのですが、その議論を進めた後だと、第一正規形もフィールド間に関数従属性を評価できる状態にするための変換であるという言い方もできるということを説明したいと思います。以前に説明した時は、フィールドにあるべき値は元々その全ての値の集合があって、その1要素が入るという前提があるという理由でしたが、見方を変えると関数従属性も理由として言えるということです。
関数従属性は、あるフィールドの値が決まると、別のフィールドの値も確定されるという関係性があるということでした。ここで、今までに出てきていませんが、データはどこかで見たことがあるような第一正規形を満たしていない表を示します。情報化を進める上で「納品書」をターゲットにしつつ、納品書そのものから頭が離れられないと、結果的にこういうデータ構造を作ってしまうでしょう。もちろん、販売明細に商品と個数(通常のカッコで記述)のセットが複数あったり単独であったりとしています。とりあえず主キーは {販売日, 販売先顧客} としますが、同一日に同一顧客に販売しないなどの制約あるとしましょう。ただし、説明の上では便宜的に行番号で行を参照することにします。

この状態の時、主キーになっている2つのフィールドはいいとして、販売明細に対して関数従属性が言えるかどうかはいかがでしょうか? どうやら商品名が見えていますが、主キーから商品名に対して関数従属があるでしょうか?例えば1行目は「ロボットいか2号」が存在しているので、その商品に決定できるという言い方もできますが、実は他の商品も明細にあるので、{2021-11-09, トイザラシ} → {ロボットいか2号} という関数従属があるとは言いづらいです。つまり、販売明細フィールドの値を1つの塊があるとしたら、{2021-11-09, トイザラシ} → {ロボットいか2号(5), ロボットねずみ3号(3)} という関数従属があるとは言えるとは思いますが、→の右側は明らかに複数のフィールド、複数のレコードという状況を示していて、仮にそれを許すとしてもドメインの記述が複雑怪奇になり、また称号もしづらそうなデータです。ここで、明らかに「商品名」「個数」という複数のフィールドがあることも明白です。
1行目は、部分的に見れば、{2021-11-09, トイザラシ} → {ロボットいか2号} と {2021-11-09, トイザラシ} → {ロボットねずみ3号} の関係性を現状では保持するとしたら、それらを別々のレコードに分離しましょう。その時、商品名と個数の組み合わせのものは、別々のフィールドで記述可能です。そうであれば、第一正規形を満たすものとして、次の表を作ることができます。この場合、4つのフィールドが全部主キーフィールドになります。区別したい基準について考えればその結論は出てくるでしょう。{販売日, 販売先顧客名} だけなら、重複したレコードがあります。つまり、何をいくつ買ったのかという情報がキーとして存在しないと、重複するレコードが存在するということになります。

商品名も個数も主キーになってしまいましたが、いずれも、関数従属性の評価が可能なフィールドになったと言えるでしょう。フィールドに重複の値があったら、複数値が意味があるのか、それらの個別の要素に意味があるのか、明確ではないということも言えます。単独の値のみであれば、関数従属性を検討する土台としては確定した値を扱えるとも言えます。
関数従属性はボイス-コッド正規形までの議論では重要な役割を持っているのですが、第一正規形を経ないと、関数従属性を議論できないというのが逆に追った場合に見えている特徴と言えます。
ここで、関数従属性についてさらに理解を深めるために、公理系の話をします。いきなり数学になり引くかもしれませんが、数学的な証明が可能な世界、つまり理屈が正しいということを言える世界が広がっていることはともかく理解してください。関数従属性についてはアームストロングの公理系としてまとめられています。以下、大文字のアルファベットは、属性の集合です。集合の基本的な記述についての説明はすっ飛ばします。
反射律:Y⊆Xのとき、X→Yが成り立つ
増加律:X→Yのとき、X⋃Z→Y⋃Zが成り立つ
推移律:X→Y及びY→Zのとき、X→Zが成り立つこれらの規則から、次の規則を導くことができます。
合併律:X→Y及びX→Zのとき、X→Y⋃Zが成り立つ
擬推移律:X→Y及びW⋃Y→Zのとき、X⋃W→Zが成り立つ
分解律:X→Y及びZ⊆Yのとき、X→Zが成り立つこれらの規則を利用すれば、全ての関数従属性が求められることが証明されているため、関数従属性は、表の特徴を完全に記述することが可能ということの理論的な背景になっていると言えます。
ここで改めて、今までに説明してきたことをさらに細かく説明をします。以下の表は途中で出てきた表ですが、輸送会社が増えているということと、前提を少し変えます。販売明細IDは連番を振っているので、これが主キーになるのはいいかと思います。一方、同一販売日に、同一顧客に対して、同一の商品は2度以上は売らない、つまり、{販売日, 販売先顧客, 商品名} についても候補キーになりうるということにします。「輸送会社」は商品に紐づいているように見えますが、ここでは顧客が指定した先ということにしますので、その意味では、同一日に同じなどのルールはないとして、その都度、レコードごとに決められるということにします。つまり、候補キーとしては {{販売明細ID}, {販売日, 販売先顧客, 商品名}} となっているということを先に示しておきます。
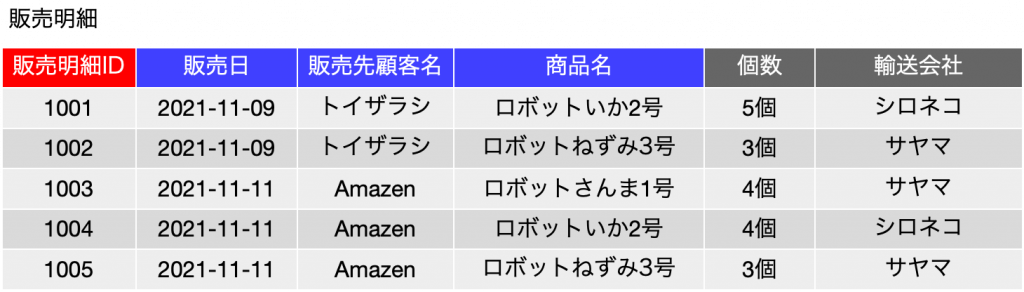
ちなにみ、この表は、ボイス-コッド標準形を満たしています。候補キー以外の関数従属性はありません。ちなみに、そのために、「単価」を取り除いていたりします。
ここで、まず、候補キーに絡んでいない、個数や輸送会社フィールドを見てみます。これらは、すでに入力されているので、1行目は何、2行目は何かということは決まっています。つまり、行を特定すれば、個数や輸送会社は特定できるので、{販売明細ID} → {個数}、{販売明細ID} → {輸送会社} という関数従属があるという見方をします。矢印の右側に同じ「シロネコ」や「4個」というデータがあるとしても、その行ではその値に決まっている。つまりは表にそのように入力されているということで、主キーから決定できる状態にあるという見方をします。
では、候補キーに絡んでいるものはどうでしょう。{販売明細ID} → {販売日}、{販売明細ID} → {販売先顧客名}、{販売明細ID} → {商品名} という関数従属があると見ることができます。これは連番を入力した販売明細IDが、レコードの特定が可能なので、候補キーに絡んでいないフィールドについてと同様に言えるということです。ということで、→の右側は、単独のフィールドとして、主キー以外のものが全部登場しました。
ここで、合併律を考えてみると、{販売明細ID} → {販売日}、{販売明細ID} → {販売先顧客名} の2つの関数従属性は、{販売明細ID} → {販売日, 販売先顧客名} にまとめることができます。これを販売明細IDを除く全てのフィールドに繰り返すと、{販売明細ID} → {販売日, 販売先顧客名, 商品名, 個数, 輸送会社} と合成ができます。つまり、{主キー} → {主キー以外のフィールド} という関数従属性が導かれて結果的に右側はレコードそのものとなります。もちろん、販売明細IDは入っていませんが、入れたところで主キーであることは変わりないので、それも結果的に同じとみなします。すなわち、矢印の左右に主キーを追加しても合併律により関数従属は整理値、左側は同一集合を合同しているので{主キー}のまま、右は全フィールドになるのです。結果的に、候補キーは以下のように、左右の全フィールドを合成すれば表の全部のフィールドになるような記述が可能であり、これによって、個別のフィールドが関数従属していることと、候補キーになりうることを示していると言えます。ちなみに、2つ目の→右側にある「商品明細ID」は、左側の3つのフィールドで十分に候補キーであるということで、右側に記述しても矛盾は生じません。各行で違うので明白かと思われます。
FD1 : {販売明細ID} → {販売日, 販売先顧客名, 商品名, 個数, 輸送会社}
FD2 : {販売日, 販売先顧客名, 商品名} → {販売明細ID, 個数, 輸送会社}スーパーキーを考えるとき、これら候補キーから、公理系を当てはめて考えれば、スーパーキー自体も関数従属の→の左側に存在可能ということが言えます。例えば、1行目に対して、フィールド輸送会社について増加律を当てはめると、次のようになりますが、矢印の右側はすでに存在しているフィールドを追加することになります。集合なので同一の要素は存在できません。よって矢印の右側は同一になります。
増加律により、以下が成り立つ
{販売明細ID} U {輸送会社}
→ {販売日, 販売先顧客名, 商品名, 個数, 輸送会社} U {輸送会社}
部分集合とのUは元の集合と変わらないので、右辺は次のようになる
{販売日, 販売先顧客名, 商品名, 個数, 輸送会社} U {輸送会社}
= {販売日, 販売先顧客名, 商品名, 個数, 輸送会社}
すなわち、次の関数従属性も成り立つ
{販売明細ID, 輸送会社} → {販売日, 販売先顧客名, 商品名, 個数, 輸送会社}このように、候補キーに対して、キーに存在しないフィールドを1つあるいは2つ以上の組み合わせで追加しても、いずれも、→の右側は残りの全フィールドとなり、レコードを特定可能であることに変わりはありません。この時の{販売明細ID, 輸送会社}は、主キーと同様にレコードの特定が可能と言えるので、スーパーキーでもあります。ただ、全部記述していると、大変なので、スーパーキーは頭の中で展開して、その中で、最小のフィールド構成である候補キーを求めるということがまずは必要になるということです。
ちなみに、前回、ボイス-コッド正規形のルールとして、「候補キーからの関数従属性ではない関数従属性は存在しない」言い換えれば「全ての関数従属は候補キーからである」というルールを紹介しました。これは、もともとコッド先生の論文で、ボイス先生と共同で提唱しているルールであり、最初はこれが第三正規形と読んでいたものです。ですが、現在のさまざまな教科書に書かれているボイス-コッド正規形のルールは「スーパーキーからの関数従属性ではない関数従属性は存在しない」言い換えれば「全ての関数従属はスーパーキーからである」となっていて、見かけの上ではより広い範囲を指すようになっています。これはコッド先生より少し後の時代、1982年にZaniolo先生が発表した論文で記述されているルールであり、現在はそちらの記述がスタンダードになっています。
次回は、スーパーキーであることを考慮しないといけない例を出して、ボイス-コッド整形を引き続き紹介します。