さて、第三正規形まで辿り着きましたが、次には第四ではなく、ボイス-コッド正規形(略してBCNF)があります。増永先生の「リレーショナルデータベース入門」によると、ボイス先生は第四と呼びたかったのにコッド先生はこれは第三の改良だろうといった議論をしていると、別の人が第四を提唱してしまったという経緯があるそうです。なので、第3.5正規形という言い方もされるようですが、ここでは「ボイス-コッド標準形」と呼びましょう。ただ、この辺りまで来ると、そもそもの定義を説明してもいきなりは理解できない領域に来ています。ということで、まず、どんな表が第三正規形を満たしているのだけどボイス-コッド正規形を満たしていないと判断するのかを紹介し、その分解の手がかりを与えているのかということを具体的に説明します。ただ、そのサンプル自体がかなり奇抜と思われる可能性は高いので、構えてください(笑。
以下の表「顧客対応」は、あるシステムで、顧客との面談対応のスケジュールを管理しているとしてください。例えば、ZOOM使っているとして、時間枠は1時間ごとに確保できるとします。となると、顧客対応の1レコードは1つの「面談」を示していると言えます。顧客に対して、何回も面談はあるでしょうけど、同じ時間には面談がないとします。つまり、顧客は同時間枠で2つ以上は確保しないという想定にします。となると、それ以外に担当フィールドを用意しましたが、例えばZOOMのURLや、メモ欄などのフィールドを用意しても、{顧客, 時間枠}によってレコードは特定できるということになります。つまり、FD1: {顧客, 時間枠} → {顧客, 時間枠, 担当}という関数従属性があり{顧客, 時間枠}が候補キーと見做せるので、主キーは{顧客, 時間枠}になります。

ところが(ここからが重要)、顧客対応する社員について、担当のフィールドに入っているように見えていますが、ここで、担当者が決まると顧客が決定するという縛りを入れます。つまり、FD2: {担当} → {顧客} という関数従属性があるということです。
ちょっと強引な設定のように思われるかもしれませんが、この状態は、キーフィールド以外から、キーフィールドの一部に、関数従属があるという状況になります。第三正規形で出てきた推移的な関数従属ではないのかと考えるかもしれませんが、実は一連の記事では正確な記述をしていない箇所がありまして、第三正規形は、{主キー} → {主キー外のフィールド} → {主キー外のフィールド} という推移的な関数従属があってはいけないというのが正しい規則だったのです。この例では、{主キー} → {主キー外のフィールド} → {主キー内のフィールド} という推移はあるとは言え、第三正規形においては想定していなかったということです。
先に更新不整合を確認しましょう。いずれも、FD2の存在を問題にすれば考えやすいです。まず、前の表から3行目のAmazenさんとの面談がキャンセルされたとします。すると、YがAmazenの担当であるという情報も失われます(削除不整合)。新たな担当者Kがトイザラシも担当することになったとします。しかし、Kが面談にアサインされるまで、その情報をこの表に入れることはできません(挿入不整合)。担当のXが退社して、トイザラシの担当がLになったとします。すると、複数のレコードに渡って修正をしなければなりません(更新不整合)。ということで、不整合はあるということが確認できました。
いずれにしても、1つの表に複数の関数従属があり、それらを表として分離することで、正規形であることを満たすことができるという考え方になります。ということで、以下のように分離できます。まず、FD2から、「顧客担当」という新しい表が登場します。元は4行でしたが、1、2行目は同一の関連性を表現しているのでまとめてしまって3行になります。そして、担当から顧客を求めることができるので、元の「顧客対応」表では「顧客」フィールドは不要になります。しかしながら、そうなると主キーを構成するフィールドの1つがなくなりますが、ここで再度考え直せば、{時間枠, 担当}を主キーとすることで顧客対応の表の1行は、「面談」を示すことができるので、この2つの表に分解した結果は、元の表が表現していることと同一とみなすことができます。つまり、担当を参照の手がかりにして結合すれば、元の表になります。分解後の顧客担当はもちろん単一の関数従属性しかありませんし、顧客対応についてもこの場合はキーフィールドしかなく、キーの間での関数従属はない、つまり時間が決まれば担当が決まるというわけではない(逆も同様)となっています。

ここで、ボイス-コッド正規形の定義として紹介したいのは、Date先生の「An Introduction to Database Systems, Vol.1」に記載されている「表に存在する関数従属性FD: {X} → {Y}について、Xは候補キーである」というものです。候補キーつまりは表のレコードを特定可能なキーフィールドの集合です。候補キーによるもの以外の関数従属、すなわち関係性があってはいけないということです。今回の最初の表において、FD2のキーである{担当}という集合は、候補キーの中にはなかったということで、元の表はボイス-コッド正規形ではないことになります。
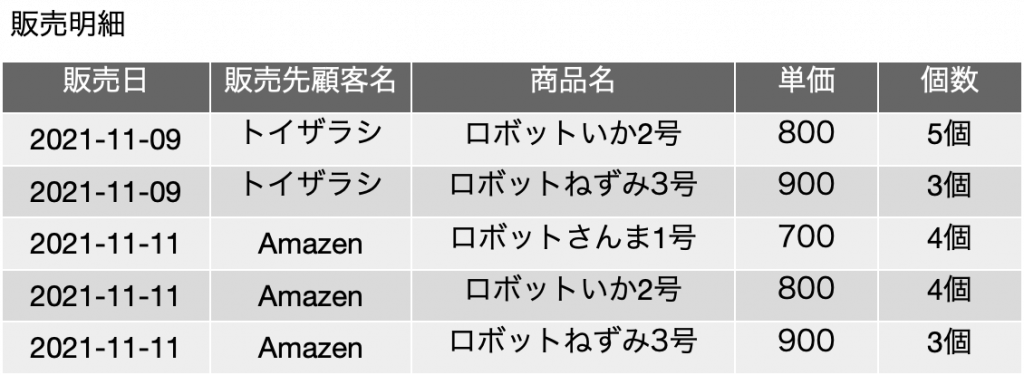
ここまで、段階的に見てきましたが、このボイス-コッド標準形の「候補キー以外のキーを持つ関数従属を分離する」という考え方は、実は第二、第三正規形の時も「成り立っている」と言えます。第二正規形で出した例はこれです。この表の候補キーは、{販売日, 販売先顧客名, 商品名, 個数} でした。この表に、FD: {商品}→{単価} という関数従属性が存在していたのですが、{商品}というキー集合は候補キーにはありませんので、分離をしたのでした。
第三正規形のサンプルは以下の表で、候補キーは{販売明細ID}でした。前の表と前提を少し変えて、同一販売日、同一顧客、同一商品、同一個数の複数のレコードが発生しうるとしており、区別するためにシリアル番号を振ったという前提が加わっています。この場合も、FD: {商品}→{単価} という関数従属性が存在していたのですが、候補キーには{商品}というキーの集合は存在しないので、分離をしたのでした。

つまり、ボイス-コッド正規形の考え方によって、第二、第三正規形の示している問題点と分解のルールは導き出せるということになります。その結果、第二、第三正規形「不要である」と結論づけている書籍もあります(Darwen, An Introduction to Relational Database Theory, 3rd Ed.)。
ところで、今回の最初に示したような表に当たったことありますか? 個人的にはかなり不思議なビジネスルールではないかと思います。このような場合、最初から表を分離してかからないでしょうか? もちろん、不思議なビジネスルールは気付きにくいということもあってのここまでの標準形の旅をしてきているということもあるのかもしれませんが、分離を前提に進めていれば、第三だけどボイス-コッド標準形ではないというような状況にはなかなかお目にかかれないと思われます。個人的にも、「あ!これは第三だけどボイス-コッド標準形ではない!」という気づきがあったことは実はありません。そういうこともあって、第三正規形までで十分説もあるのではないかと思います。ですが、第二や第三については、表の中に埋もれている関数従属性についての詳細な検討をする機会にもなるので、学習する上では順番に進めるのが良いと思われます。
Abiteboul先生らの「Foundations of Databases」では、ボイス-コッド正規形の解説の見出しに「同一の事実を2度書くな」(Do Not Represent the Same Fact Twice)と書いてあり、これが正規形を導く本質なのではないでしょうか。つまり、前の表であれば、ロボットいか2号が800円という事実が複数登場するわけです。しかし、表を分ければそれは1回の記述で済むということです。ちなみに、Foundations of Databasesはこちらのサイトより個人利用に限ってダウンロードできます。
ここまでの表の分解は、結果的に「多対1」を探してきて分解をしているということに他ならないわけです。その1に対応する存在を見つける手がかりが、関数従属性という考え方になります。一旦表にしてから検討するということをずっと続けてきましたが、理屈を理解すれば、1対多の関係を見つけて表に分解するということを早期に可能ですし、分解したものが元に戻る、つまり複数の関係を絡めた表が作れるということも考えながら進めることで、データベース設計に進むことができます。しかしながら、表を分割できるということの理論的な背景は、正規化の議論の中にあります。つまり、表は分割可能であるということが証明されているというところで、現在のリレーショナルデータベースが存在していることが重要で、その理論を詳細に追うと、正規化の議論は避けて通れないということです。詳細を知らなくても設計はできるという考え方もできるのですが、その時に出てくるさまざまなノウハウっぽいことは、実は全て背景には正規化を始めとしたデータベースのさまざまな理論が関わっているのです。