このシリーズの記事は、最初はわかりやすい話が多いのですが、だんだん難しくなってきています。Facebookのいいねが次第に減り、Twitterのリツイートする顔ぶれが変わってきていますが、頑張って続けたいと思います。
さて、前回のキーフィールドの話をしましたが、キーフィールドはnullを取らない前提があるという話を書いておくべきでした。nullは何と比較してもfalseになるので、照合できないから、キーフィールドの値に使えないのです。nullを許すと、照合出来ない、すなわち検索が出来ないレコードが発生するので、キーフィールドによってレコードを特定するという前提が崩れるのです。ちなみに、MySQLだと、論理式の値にNULLがあれば、結果は必ずNULLになります。「SELECT NULL=NULL;」は、NULLを返し、結果的にfalseとみなします。PHPだと通常はnullかどうかを確認するのはis_null関数を使いますが、null == nullの結果は1つまりtrueになります。SQLと言語ではnullの考え方に違いがあります。
前回に関数従属性という考え方を紹介しましたが、ここで、さらに厳密な「完全関数従属」という考え方をまず説明します。関数従属は、あるフィールドの値が、別のフィールドの値により決まるという考え方でした。この時、元になるフィールドの集合の真部分集合をキーフィールドとして関数従属性が成り立っていないような場合を、完全関数従属していると表現します。ざっくり言えば、フィールド同士の関連の中に、異質な関連が混ざっているような感じでしょうか? そして、第二正規形は、第一正規形が成り立つと同時に、キーフィールドに含まれていないフィールドが、それぞれの候補キーに対して完全関数従属している場合のことです。
ややこしいですね。具体例で細かく見ていきましょう。以下は前回の登場した販売明細の表です。赤いボックスは主キーフィールドを意味しています。
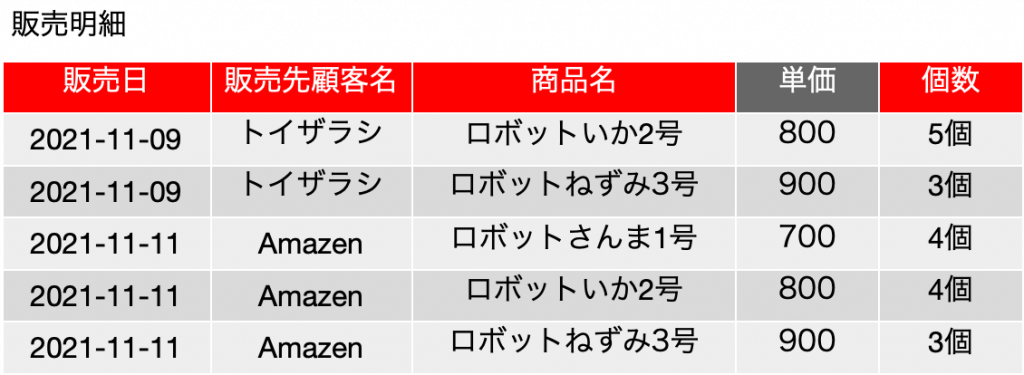
これだけのフィールドしかない場合は、候補キー、主キーとも、{販売日, 販売先顧客名, 商品名, 個数} の4つのフィールドを含むものしかありません。よってこの1つの集合に関して完全関数従属しているかどうかを調べるのですが、ここで、FD: {商品名} → {単価} という関数従属があるとします。つまり、商品が決まると、単価が確定すると考えることにします。この辺り、前提条件次第で結果が変わりますので、前提条件をきちんと把握してください。
新たに認識した関数従属のキーフィールドである{商品名}は、候補キーとなっている{販売日, 販売先顧客名, 商品名, 個数}の真部分集合です。完全従属性の定義を検討すると、『元になるフィールドの集合の真部分集合をキーフィールドとして関数従属性が成り立って』います。完全関数従属はそれが否定されないといけないので、完全関数従属していません。また、候補キーに含まれていない{単価}が決定されるという関数従属なので、第二正規形の定義が崩れます。よって、この表は第二正規形を満たしていません。
まず、第二正規形を満たすにはどうすれば良いかということを考えますが、結論は表を分離します。キーフィールドの真部分集合の関数従属が表の中に登場しないように表を分離します。つまり、単価を切り離せば良いということになります。ここで、表は分離して、後から結合できるという事実があり、この辺りは数学で記述するのはかなり難しい話になりますが、このシリーズのだいぶん前に実例で感覚的に説明をしているので、これは既知の事実だとします。つまり、以下のようになります。新たに出てきた商品の表の候補キー、主キーはいずれも{商品名}であるとします。
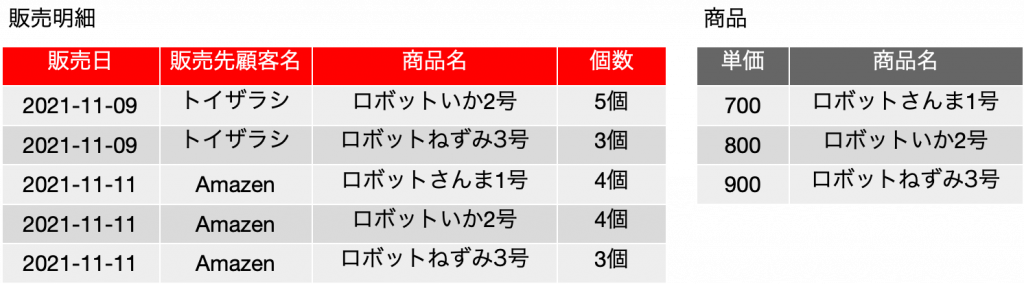
販売明細は、候補キー、主キーとも、{販売日, 販売先顧客名, 商品名, 個数} の4つのフィールドの集合になります。ただし、そのどの真部分集合を考えても、関数従属性は存在しません。よって、単価を分離し、商品名で照合して元のデータが得られるという状況にすることで完全関数従属性が成り立ち、第二正規形を満たすことになります。
要するにマスターを分離することか?と言われればそうです。ただ、この段階で、全てのマスターが分離できるわけではありません。さらに別の正規化のルールも必要になります。
前回、同じような表で以下のようなものも提示しました。こちらは「販売明細ID」フィールドがあります。ここで、この表の前提を少し拡張します。前回のキーフィールドの議論では、販売日〜個数のフィールドには重複するレコードがないという前提を引き継ぎましたが、それをやめてみましょう。良し悪しの問題はちょっと目を瞑って、番号を振ったのだから、区別できるでしょうという大雑把な設計方針が導入されたと思ってください。{販売明細ID}を候補キー、主キーとして、{販売日, 販売先顧客名, 商品名, 個数}は、もはや候補キーではないと前提を変えてみます。
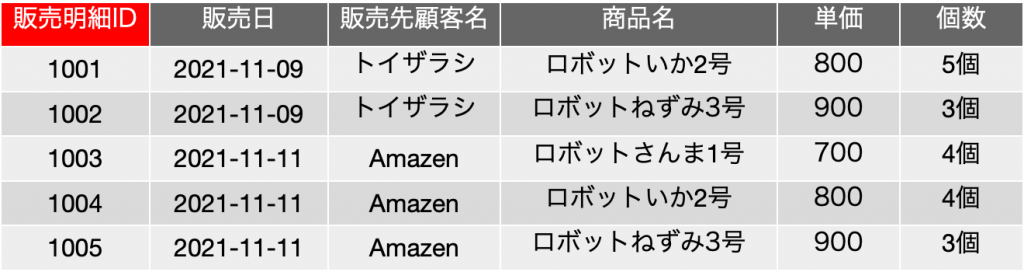
単一のフィールドが候補キーであり主キーであるような状況は意外にシンプルです。ここで、関数従属性はどうなるかというと、例えば、販売明細IDが1003だと、販売先はAmazen、商品名はロボットさんま1号など、残りのフィールド全て、1つのフィールド販売明細IDが決まれば決まっているということになります。つまり、関数従属としては、FD: {販売明細ID} → {販売日}、FD: {販売明細ID} → {販売先顧客名}、FD: {販売明細ID} → {商品名}、FD: {販売明細ID} → {単価}、FD: {販売明細ID} → {個数}、といった関係があるとみなされます。これも厳密に記述すると、FD: {販売明細ID} → {販売日, 販売先顧客名, 商品名, 単価, 個数} ということになり、矢印の右側の集合の部分集合を持つ関数従属性が大量に存在するということになります。つまり、販売明細ID単独で、レコードの特定が可能となっているということです。
であれば、候補キーの真部分集合はありますか? 単一の集合の真部分集合は空集合を除いてあり得ません。空集合は実はnullなので、これはキーとしては排除するのが定義でした。ということで、真部分集合の関数従属は存在しません。もう一度、完全関数従属の定義に立ち返ると『元になるフィールドの集合の真部分集合をキーフィールドとして関数従属性が成り立っていない』であり、まさにその通りなので、実はこの販売明細IDを主キーにした表は、すでに第二正規形が成り立っています。なお、商品が決まれば単価が決まるという事実は存在していて、FD: {商品名} → {単価} という関数従属性はあるとしても、こちらの表では{商品名}という集合は、候補キーの集合{販売明細ID}の新部分集合ではないので、完全従属性は保持されています。不思議ですが、ここで、{販売日, 販売先顧客名, 商品名, 個数}は主キーではなく、それらが重複するようなレコードの存在を肯定したという状況の変化があったので、実は表としての性質が変わってしまっているということです。
ふと思うのは、Excelの表って、最初から行番号が振られているので、第一正規形をクリアすれば、行番号を主キーと見做せば自動的に第二正規形も成り立つってことになりますね。
あれ?じゃあ、マスターって分離できないのか?と思われるかと思いますが、後半に示した表から商品マスターが取り出されるのは、実は第三正規形を満たすためのテーブル分離で実現されます。次回は、なぜ正規化が必要なのかという議論に必要な更新時異常という考え方を紹介し、さらにその後に第三正規形の説明をしようと思います。