データベースの話を進める上で、基本的な概念として何をベースに話をスタートさせるかをきちんと決めておきましょう。用語の整理というよりも、基本概念の整理がまず必要です。以下の図は、どこかで見たことがあるようなと思われる方もいらっしゃいますが、大して難しい概念はないと思います。まず、これを見て、直感的に、住所録、つまり複数の人の名前、住所、電話番号を「表にしている」と見てもらえると思います。
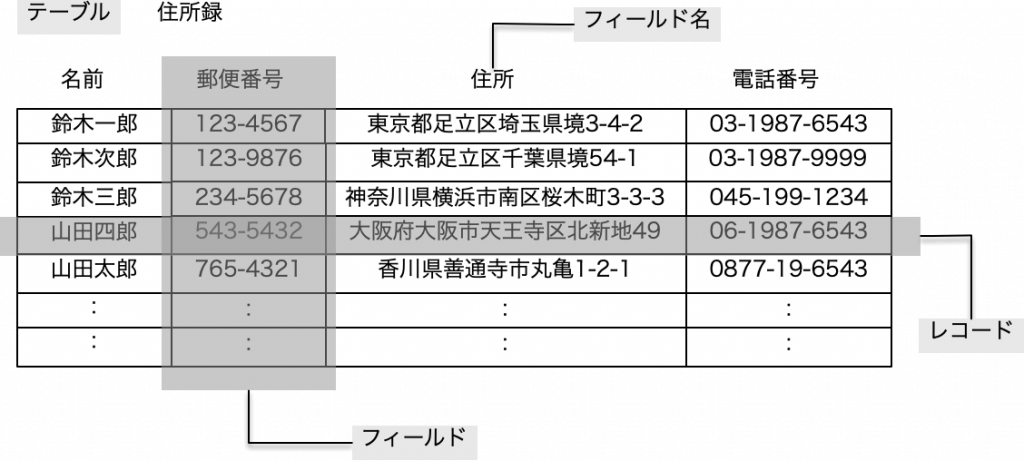
この表がデータベースのごく基本的なモデルとなります。表にまとめることで、人間がデータを参照したときに理解、あるいは活用がしやすくなるということがあります。データがを混沌と記録していたとして、記録はできているとしても、そこから特定のデータを探したり、データの傾向を求めるということは大変なことだったり失敗したりということになります。一方、データをきれいに整理しておけば、容易に検索したり、確実に集計したりということが期待できます。その整理された形式が表です。
ここで、Excelなどの表計算ソフトを引き合いに出して、「表は良い」ということを議論することもできるでしょう。表にしておくことで、オーバーな言い方ではありますが、多くの人が成功体験を積んでいるはずです。色々な利点が見出されている表というのものをモデルとして考えるということが出発点になります。もっとも、それは鶏と卵の議論ではないかということも言えるかもしれません。リレーショナルデータベースの理論が最初に発表されたような時期だと、表というモデルを考えること自体は単に1つのアイデアであり有用性までは実証されていないとの見方もあったようです。後々、ソフトウエアとして実装された上で、リレーショナルデータベースの有用性が証明され、理論と実際が相互に発達してきたという経緯もあります。
結果的に「まず表で始めます」となると、表が便利なのは常識だろうということで理由が吹っ飛んでしまいますが、表が便利なことを突き詰めて考えるのはやはりかなり難しいとも言えます。感覚的に、理解しやすく、しかも、大量のデータを扱えそうだというあたりの考えが出発点にあるということは、それほど不自然ではないと考えます。
さて、表とは言ってももう少しその構造を細かく見ましょう。非常に重要なことは「1人の人が1行」ということです。つまり、この行のことを「レコード」と呼ぶとして、1レコードが何を表しているのかということが非常に重要です。実は、これが決まればデータベースは実装可能ですが、1レコードを示すものが揺らいだり、間違っていると、データの記録がうまくできません。このことは改めて説明しますが、ここでは住所録は1レコードが1人であるということに注目します。そして、1人のレコードには、複数の「フィールド」があります。フィールドには「フィールド名」がつけられています。
1人の人の住所録を管理する上で、ひたすら名前や住所を書き並べても良いのですが、よく整理された状態というのは、一定の基準で情報が分離され、整頓されているということであると言えます。基本的に1人の人は、1つの名前があって、1つの住所があるということにここではしてください。だとしたら、名前と住所をごちゃ混ぜに記録するよりも、名前の枠、住所の枠で分離しておく方が、整理されたように見えます。つまり、ある特定の「属性」の情報「だけ」が取り出したりあるいは入力しやすくなっている方が都合が良いということが言えるはずです。もし、ごちゃ混ぜだったら、その混沌としたデータから一部分のデータ(例えば、名前だけ)を取り出すことが大変だったり、あるいは不可能だったりします。よって、フィールドに分離分割され、フィールドに実際のデータを入れておくという仕組みが作られたわけです。そして、フィールドという単位で処理をすることにより、うまくいけばデータの種類に関わらず、必要なデータだけがポンと出てくるということができるはずです。
ちなみに、レコードについては、行、ロー、タプルなどの言い方があり、フィールドについては、列、カラム、属性、アトリビュート、プロパティなどの言い方もありますます。一部のコミュニティではその言い方を間違えると白い目で見られるということも以前はあったようですが、表形式でデータ全体を考えるという概念上は概ね同じものを指しています。一連の記事では、レコード/フィールドという呼び方で進めます。
表計算ソフトだと、縦横にセルが並んでいるのですが、見かけは同じ表でも、データベースでの表は、まず、表をレコードごとに分割されていて、そのレコードにフィールドが存在するという見方をするのが良いでしょう。表の一部分を自由に扱うということもある意味はできますが、階層的に記述したら、以下の図のように、レコードの方が上位概念になります。この図の線は、正確には「導出可能」という意味です。ある表である「住所録」があるとき、その住所録からレコードに辿り着き、特定のレコードからフィールドのデータに辿り着けるというのが導出の具体例です。実際にそういうプログラムを記述できると言っても良いでしょう。視覚的にいえば、表をまず横方向にスライスして、そのスライス1つ1つについて、縦方向にスライスすることで実データに辿り着くという感じです。
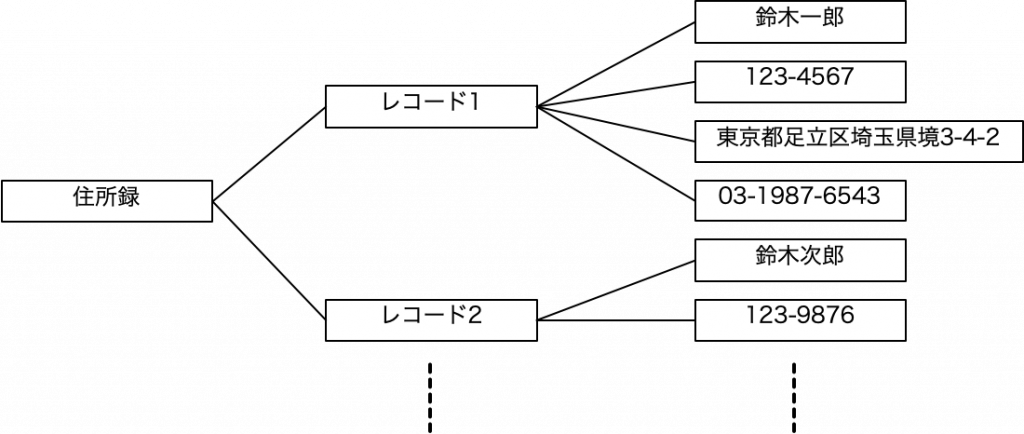
階層の図(「ツリー」と呼びましょう)ではフィールド名は省略していますが、最初の表と、この階層図は、概念的には同じものを示しています。同じとは何か? ここでは「同一データ」と言っても良いでしょう。「表とツリーは同一である」ということは理解しづらいことかもしれませんが、一方で当たり前すぎて意識していない人も多いかもしれません。住所録は表で記述できますが、ツリーでも記述できるので、同一なのです。もちろん、表のほうがコンパクトで扱いやすそうです。ツリーが優れている理由はここでは明確にはありませんが、ツリーは関連性を明示可能です。つまり、表/レコード/フィールドという階層を明確に示すことができています。
ツリーを見ていると、フィールドの集合がレコードであり、レコードの集合が表であるということが明確にわかります。ここで、フィールドだけが具体的なデータを記録できていて、レコード自体はそのフィールドの集合という位置づけになります。なので、もちろん最初のレコードを「鈴木一郎」という名前で呼んでもいいのですが、レコードを特定する情報はここでは明確ではないので、便宜的に「レコード1」と記述しています。なお、レコードの特定の問題については、今後、色々な視点で説明をすることになります。
集合(set)といえば数学、数学といえば「嫌い」という人も多いかもしれませんが、集合論の真面目な議論に入らなくても、日常的な感覚の範囲では頑張って理解しましょう。ただ、集合と言うと深い議論があって、その1つは「集合には要素に重複はない」と言う定義です。集合の基本的な定義は「お互いに区別できるものの集まり」となっています。住所録の場合、重複したデータ、つまり全く同一の2つの行があった場合、用途上それは2つ存在している必要は全くなく一方は消したりないものとして扱うことは問題ありません。なので、レコードの「集合」が表なのです。また、フィールドについても、1つしかない名前を2つ以上のフィールドに入れたところでそのうちの1つしか必要ないので、フィールドの「集合」がレコードになるのです。この辺り、現実と数学の定義がよく合います。集合の考え方がリレーショナルデータベースの理論の基礎になっているという点は決して無視できない時事です。ここでは細かく議論しませんが、集合の要素は順序は問わないという定義もやっぱりデータベースの表といろんな意味でよくマッチングします。ちなみに、今回は数式は出しませんでしたが、先々では数式も出ると思います。その方がわかりやすいこともありますので、その時はなるべくわかりやすく説明するように心がけますが、数式があっても驚かないでください。
数学としての集合は有名ですが、その仲間のようなものも数学で定義されています。要素の重複を許すものをバグ(bag)あるいは多重集合(multiset)と呼ばれています。また、重複を許しつつ順序も情報として持つものを列(sequence、list)と呼ばれています。さらに重複は許さないが順序も情報として持つ順序集合(ordered set)もあります。これらも集合を基にした数学の理論は展開されています。ですが、プログラムができる方は、むしろ配列などとして理解されており、物理的な意味でデータを実際にこの形式で扱っているとも言えるので、抽象数学よりも具体的な世界での理解はされているのではないかと思います。数学に興味のある方はその辺りも書籍などを当たってみると良いでしょう・・・と言いつつ、この種の数学の書籍はかなり気合いと時間をかけないと理解に至らないのは確かですね。
次回は、表をツリーにしたことで、ER図の一部の定義に到達できることを説明しましょう。