1対多、1対1と話が進んできました。関係としては、他には多対多があります。ちなみに、多対1もあるという話もあるのですが、ほとんどの場合、双方向で検討が可能なので、1対多と多対1は、単に説明の時に適切に参照するためのものになります。例えば、「納品書と販売明細は1対多の関係にある」と「販売明細と納品書は多対1の関係にある」と説明していることは基本的には同一と考えられるからです。
多対多をこれまでの実例の中で探そうとしても、実は存在していないので、全く異なる事例を出します。この多対多が発生する代表的な例題は、学校の中のデータ管理です。学生1人1人を1レコードとする「学生」表と、履修科目1つ1つを1レコードとする「履修科目」表があったとします。それぞれ、主キーフィールドの〜IDをあらかじめ設けてあります。
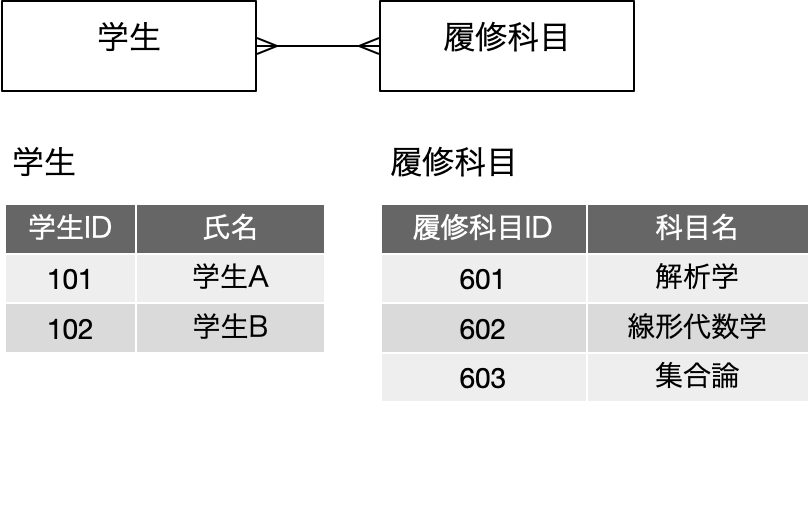
これがどう多対多なのかというと、オブジェクト図と表へのデータ追加をしてみて検討することができます。例えば、学生Aは、解析学、線形代数、集合論を履修するということで、学生から見た履修科目は1対多の関係にあります。一方、線形代数学を履修する学生は学生Aと学生Bで、これもやはり1対多の関係にあります。双方とも、ボックスから複数の線が出ているオブジェクトが1つ以上は存在します。実際の大学のデータだと、このボックスが大量に発生して手で描きにくいですが、2人3科目くらいならまあ大丈夫かなと。このように、どちらから見ても多の関係が発生する可能性がある場合、多対多であるとみなします。ここで、それをどうデータ化するという話が実はちょっと込み入るのですが、以下の図の下半分の表のように表現したとしましょう。すでにIDが振られているので、それを利用しています。学生、履修科目、いずれも対応する表との複数の関連性があるので、複数のID値を覚えておかないといけませんが、表の上で見やすい便宜上の記録として、ID値をカンマで区切るということをおこなっています。
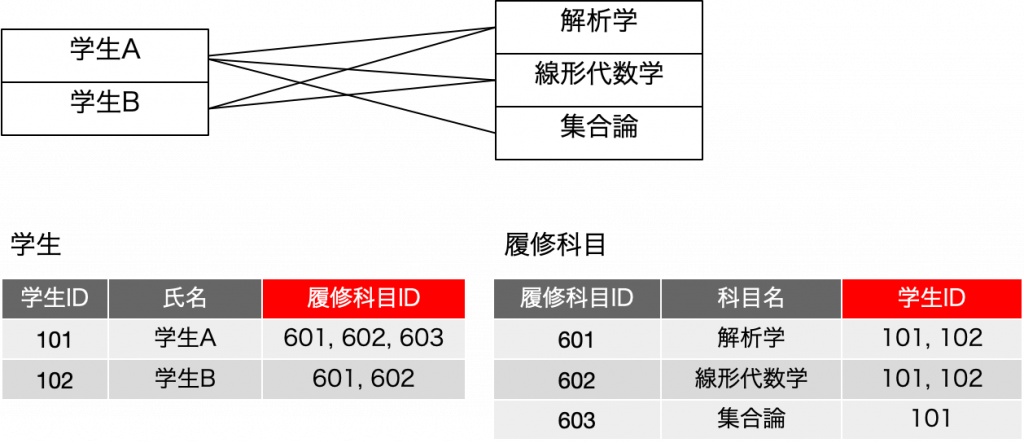
学生Aの履修科目は、101 → {601, 602,603} となっています。つまり、右の表の3つのレコードいずれも参照しているということになります。集合論の履修学生は、603 → {101} であり、一人だけが履修していることも表現されています。ちょっと見づらいとは言え、ともかく、学生と履修科目の関連はなんとなくうまく表現できていると思えます。ただし、問題はあって、ある学生がある科目を履修する場合、2つの表の〜IDをそれぞれ矛盾なく更新しないといけないなど、データの処理は面倒になります。これも、CRUDをそれぞれ考えれば、ちょっと大変そうですが、ともかくロジックが加わります。
ただ、この表を見ていて、何が問題かというと、データベース設計を少しでもかじった方は明白なように、〜IDのフィールドに複数のデータがあるため、第一正規形を満たしていないということです。第一正規形は、フィールドの値が1つの素な値、言い換えれば表の中に表があるような状態を認めないという考え方です。「素な値」というのはちょっと唐突で、これもいずれ説明したいとは思っていますが、ここでは表の中に、また表があるという状況になっているとも言えます。この内在する表をうまく外部に出すというのが第一正規形の1つの変換方法になります。一般には、その結果、表のレコードが増えることになるのですが、そこから表の分割は第二、第三正規形の適用になります。ちょっとここでは詭弁っぽいかもしれませんが、すでにIDを振っているあたり、第三正規形まで満たしている状態でもあるので、その状態を有効に活用したいと思います。
改めて学生の方を見ると、学生IDと履修科目IDの1つのデータは、101 → {601, 602,603} となっています。これは、101 → 601、101 → 602、101 → 603 といった3つの関係に分離できます。この関係だけを「履修登録」表にまとめてみると次のようになります。学生の「履修科目ID」からこの表は作ることができますが、一方、履修科目の「学生ID」からも実質的に同一の表を作ることができます。つまり、双方にIDのカンマ区切りリストを持っているということは、データが重複していたのです。重複していたので、更新時には両方を変更しないといけなかったということもここでわかります。また、同一の表を2つ持っている必要は全くありません。なので、一方の表を残すと、結果的に1つ表が増えると同時に、元からあった2つの表から双方を参照する〜IDフィールドを削除することができます。
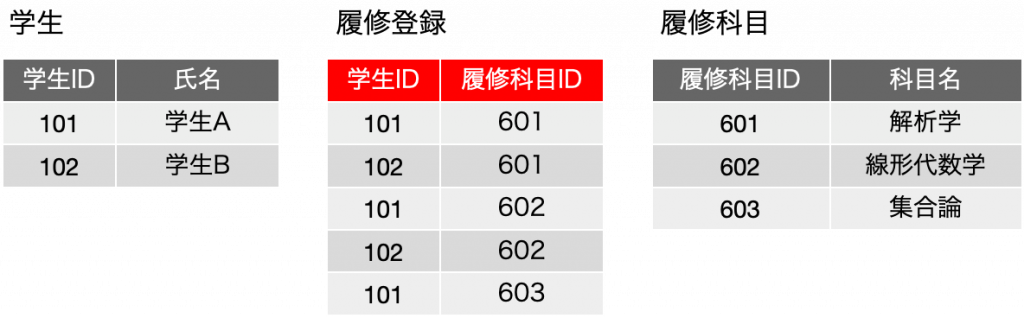
学生の履修科目IDや、履修科目の学生IDを消しても問題はありません。この3つの表をあらためてよく見てください。学生Aは、学生IDが101です。履修登録で、学生IDが101のレコードは3つあります。その3つのレコードの履修科目IDを順番に見ると、601、602、603です。つまり、履修登録レコードに3つのレコードがある学生は、3科目を履修しているということが、データとして表現されています。そして、どの科目かということも、履修科目IDの値から求めることができます。これもやはり表と表との結合で求めることができるので、「まとめた表」を生成することが可能です。さらに、履修登録にレコードが存在することが「履修登録されている」という事実を表しています。学生Bが集合論を履修していないことは、{201, 603}というレコードが存在しないことから決定づけられます。
ここで、この3つの表の関係をあらためて見てみると、学生からみた履修登録は、1対多になります。逆に履修登録の1レコードは、1つの学生だけを記録するので、1対1です。1対多と1対1なので、学生と履修登録の関係は、1対多とするという話は2回前に説明した通りです。同様に、履修登録と履修科目も同様に多対1の関係になります。ER図的に表すとこのようになります。

このように、「関係を構築する」ための表を用いる必要が出る場合も、設計をしていれば登場します。1対多や1対1に比べて複雑になるのですが、この関係における表の抽出が設計段階にできていないと、実装が大変複雑になるか、あるいは破綻するかのどちらかです。ただ、要求だけを検討してもなかなかわかりにくいです。その場合は、ともかく表にしてみる、あるいはオブジェクト図を書いて実データとしてうまく記録できているのかなどを確認します。
ちなみに、こうした関係を「作文できる」という見方もできます。つまり、ここでは「学生は、履修科目を、履修登録する」という感じです。日本語だと最後に述語が来ますが、英語だとA student resisters a subject. つまり、主語、述語、目的語の順番になって、ちょうどER図の並びの通りになったりします。そして、両側が名詞、中央の関係を記述した表に対する表現は動詞で可能です。作文が意味があれば、おそらくはこの設計は何か正しいものを表現していることになります。ただ、作文による考え方はあまり包括的ではありません。納品書と販売明細のような場合はどうなるでしょう。「納品書は、販売明細を、持つ」とかになって、動詞というか、関係性を表現する単語がなんとでも意味を考えられるようなものになってしまうかもしれません。それでも関係が明白なら、いいのですが、動詞部分が「管理する」とか「記録する」のような、表にする限りは当たり前だろう的な動詞を割り当ててもあまり意味はないのかもしれません。なので、作文可能性は参考程度のものです。ちなみに、たくさんの表が関連しているような場合、直接関連していないけど、線を辿ると関連しているような2つの表についても、多くの場合作文は可能だったりします。
ここで、学生の科目履修だから、やはり得点の記録は必要だとなりました。さて、どこに記録しますか? 科目の得点だから「履修科目」と思った方はアウトです。もちろん、解析学が80点などと記録されますが、得点は学生ごとに異なります。履修科目に記録するには、また、最初のような第一正規形を満たさないフィールドを作るしかなくなります。同様な理由で「学生」の表に追加するのもだめです。もう結論は見えていますが、もう少し得点というデータの性質を考えてみましょう。得点は、学生ごと、科目ごとに割り当てられます。となると、ここまでの検討した結果で言えば、「学生ごと、科目ごと」に履修登録がされるという状況が作られているので、履修登録の表に得点があるというのが1つのアイデアです。つまり、表で書くとこうなります。
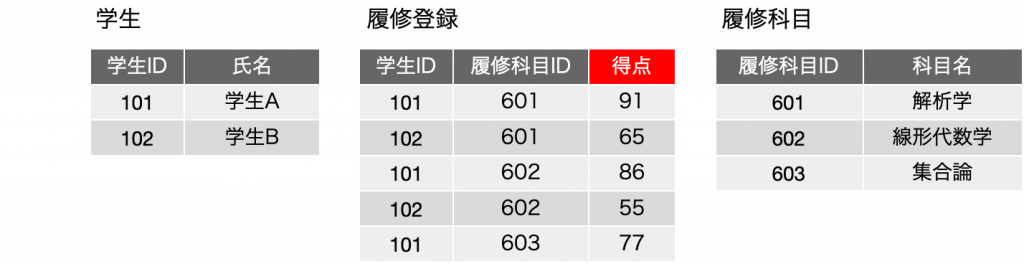
得点という情報は、履修が前提であるという考え方とも一致します。つまり、履修登録と得点は1対1であるともみることが出来て、つまりはフィールドでいいというのは前回に説明した通りです。
この多対多の関係は2つの1対多の関係にするという手法は「中間テーブル」などと呼ばれて、SQLでの設計手法では必ず登場するテクニックです。ですが、この中間にあるテーブルは単に2つの表の関連付けだけを行うだけでなく、ここに示した「得点」のように何らかの実データを持たせる必要が出る場合もあります。したがって、単なる中間にある存在ではなく、意味があって存在しているのです。この意味をうまく汲み取って表の名前を付ける必要があります。また、いろんな開発手法がありますが、この中間テーブル手法は、名前や適用方法、適用範囲を変えて、設計手法には必ず存在していると言っていいでしょう。
ということで、まずは多対多の中間テーブルによる展開を説明しましたが、何だかスムーズすぎませんか? 途中にも言いましたが、最初からID番号が振られているのは、ちょっと恣意的ではあります。ですが、まずは理解するためにそういう状況から初めてみました。中間テーブルというテクニックがあるものの、実は、第一から第三までの正規形を適用するということで、自動的に中間テーブルが登場するというのが本来の説明になるのでしょうけど、次回はそういう意味での説明をあらためて試みます。